Home / Journal / Interdisciplinary Education and Psychology
Teacher Enthusiasm, Supportive Instructional Practices, and Student Motivation in Mathematics Classrooms
teacher enthusiasm Student support Mastery goal orientation Behavioral engagement
Marthe C. Frommelt, Ulrich Schiefele, and Rebecca Lazarides
DOI: 10.31532/InterdiscipEducPsychol.2.3.005 16 Apr 2021
Abstract
This longitudinal study examined the relations between teacher enthusiasm, supportive instructional practices, and students’ mastery goal orientation and behavioral engagement in mathematics. All variables were assessed by means of student reports. A total of 751 9th and 10th grade secondary school students from 46 mathematics classrooms were presented with questionnaires at the beginning (Time 1) and the middle of the school year (Time 2). Structural equation analyses revealed that student-perceived teacher enthusiasm at Time 1 predicted student-perceived support for autonomy, competence, social relatedness, and subject matter relevance at Time 2. Student-perceived support for autonomy and social relatedness (Time 2) were related to students’ mastery goal orientation and their behavioral engagement (Time 2). Moreover, student-perceived teacher enthusiasm (Time 1) indirectly predicted students’ mastery goal orientation (Time 2) via student-perceived support for social relatedness and autonomy (Time 2). The findings contribute to research aimed at identifying teacher characteristics and instructional processes that promote student motivation.
Keywords
Teacher enthusiasm, Student support, Mastery goal orientation, Behavioral engagement
Introduction
Recent years have seen an upsurge in research exploring the effects of teacher motivation on student motivation for learning and the mediating role of instructional practices (e.g., Butler & Shibaz, 2014; Fauth et al., 2019; Kunter et al., 2013; Lazarides et al., 2018; Schiefele, 2017; Schiefele & Schaffner, 2015). Various facets of teacher motivation, such as professional interests (Schiefele, 2017; Schiefele & Schaffner, 2015), goal orientations (Butler, 2012; Butler & Shibaz, 2014), self-efficacy (Fauth et al., 2019; Lazarides et al., 2021; Praetorius et al., 2017), and enthusiasm (Fauth et al., 2019; Kunter et al., 2013) have been examined for their contributions to instructional practices and student motivation. Overall, these studies suggest that highly motivated teachers adopt specific instructional practices, which in turn promote student motivation. With the exception of only a few studies (e.g., Kunter et al., 2013; Lazarides et al., 2018, 2021; Lazarides & Watt, 2015), however, most of the findings are based on cross-sectional data and cannot provide information on the directionality of the relations between teacher motivation, instructional practices, and student motivation. Moreover, the few studies that have examined the effects of teacher enthusiasms on student outcomes have considered a rather limited range of instructional practices.
The present study aims to extend current research on teacher motivation by longitudinally investigating the relations between student-reported teacher enthusiasm and students’ perceptions of various supportive behaviors of their teachers referring to students’ experience of autonomy, competence, social relatedness, and subject matter relevance. In addition, students’ mastery goal orientation and behavioral engagement in mathematics were included as outcome variables. According to research findings based on self-determination theory (Deci & Ryan, 2000; Ryan & Deci, 2002, 2020) and achievement goal theory (Urdan & Schoenfelder, 2006; Senko, 2016), supportive instructional practices are assumed to play an important role in fostering student motivation (e.g. Bieg et al., 2011; Lüftenegger et al., 2014). Thus, investigating whether and to what extent teacher enthusiasm indirectly relates to student motivation through the use of supportive instructional practices represents the main goal of the present study.
In the following, we first present a brief review of recent conceptualizations of teacher enthusiasm and introduce the motivational outcome variables studied, students’ mastery goal orientation and behavioral engagement. Then, we discuss empirical findings on the relations among teacher enthusiasm, instructional practices, and student motivation.
Teacher Enthusiasm
In the tradition of research on teaching effectiveness, teacher enthusiasm was mostly understood as teachers’ (nonverbal) behavior conveying the importance and intrinsic value of learning and the learning material to students (Murray, 1983; Patrick et al., 2000; for a review, see Keller et al., 2016). As such, teacher enthusiasm represents a particular instructional practice aimed at increasing students’ motivation and learning engagement. This practice involves, for example, that the teacher emphasizes the value of the learning material or expresses his or her own interest in the subject being taught. Accordingly, several studies observed that enthusiastic teaching behavior is positively associated with students’ intrinsic motivation (Patrick et al., 2000), interest (Keller et al., 2014), active learning and engagement (Patrick et al., 2000), and level of enjoyment (Frenzel et al., 2009).
More recently, Kunter and her colleagues (Kunter et al., 2008, 2011) redefined the concept of teacher enthusiasm as an affective component of teacher motivation that “reflects the degree of enjoyment, excitement, and pleasure that teachers typically experience in their professional activities” (Kunter et al., 2008, p. 470). More specifically, Kunter et al. (2011) proposed two dimensions of teacher enthusiasm. Subject enthusiasm is understood as the excitement about the subject matter being taught (e.g., mathematics), whereas teaching enthusiasm describes the excitement about teaching itself. Both dimensions of enthusiasm can co-occur within the individual. According to Kunter et al. (2011), both forms of teacher enthusiasm represent dispositions of the teacher that can manifest itself in enthusiastic teaching behavior. As such, teaching- and subject-related enthusiasm can be regarded as determinants of instructional behaviors that serve to foster students’ intrinsic motivation and learning engagement.
Student Motivation and Engagement
The focus of our study is on two important student motivation variables: students’ mastery goals and behavioral engagement. According to goal orientation theorists, mastery goals represent a highly adaptive form of motivation (Barron & Harackiewicz, 2001; Butler, 2006; Pintrich, 2000). Students with a mastery goal orientation strive for constant improvement, development of new skills, and deep understanding of the subject matter. Whereas mastery goals refer to the internal motivational beliefs that might be able to explain why and in what ways students strive to attain competence, students’ behavioral engagement can be understood as the behavioral manifestation of motivation (Wang et al., 2019). More specifically, behavioral engagement refers to students’ readiness to show effort and persistence in their work for school (Elliot, 1997; Guan et al., 2006). Previous research demonstrated that students’ mastery goals promote a variety of important outcome variables such as students’ use of learning strategies, subject interest, and the choice of challenging tasks or future courses (e.g., Barron & Harackiewicz, 2001; Harackiewicz et al., 2000; Pintrich, 2000; Wolters, 2004). Moreover, numerous studies confirmed the positive association of students’ behavioral engagement with academic success (cf. Reyes et al., 2012; Wang & Fredricks, 2014) and school completion (cf. Archambault et al., 2009; Wang & Fredricks, 2014).
Teacher Enthusiasm and Instructional Quality
Theoretically, it is to be expected that teachers who are enthusiastic about teaching are more likely to adopt high-quality teaching methods than teachers who are less enthusiastic. Indeed, several studies have confirmed this assumption (e.g., Kunter et al., 2008, 2011, 2013). Moreover, teaching enthusiasm was found to be more strongly associated with higher levels of teaching quality than subject enthusiasm. For instance, Kunter and colleagues (2008) showed by means of cross-sectional data that student reports of (a) teachers’ monitoring of student behavior and (b) teachers’ provision of social support (e.g., taking care of students’ problems) are both positively associated with teacher reports of teaching enthusiasm but not subject enthusiasm. Also based on cross-sectional data, Lazarides et al. (2018) were able to find significant relations between student-perceived teacher enthusiasm
(assessed as a combination of teaching enthusiasm and subject enthusiasm) and student reports of mastery-oriented instruction. Teacher reports of teaching enthusiasm and subject enthusiasm, however, did not predict student-perceived instruction and student motivation. Moreover, also by employing a cross-sectional study design, Cui et al. (2017) showed significant relations between student reports of teacher enthusiasm and autonomy support.
In a longitudinal study, Kunter et al. (2013) focused solely on teaching enthusiasm and confirmed class-level effects of teachers’ self-reported teaching enthusiasm on student reports of their teachers’ provision of learning support (e.g., providing adaptive explanations) and classroom management. In addition, students in classes with enthusiastic teachers reported more enjoyment and greater achievement gains in mathematics one year later. Moreover, the authors were interested in exploring the mediating effects of specific teaching behaviors and found that the positive class-level effect of teaching enthusiasm on students' mathematics achievement was mediated only by student-perceived classroom management, whereas the positive class-level effect of teaching enthusiasm on students' mathematics enjoyment was mediated by student reports of both classroom management and teacher-provided learning support.
The impact of teacher enthusiasm on teaching quality was also demonstrated in comparison to other teacher characteristics (cf. Baier et al., 2019; Kunter et al., 2013). Baier and colleagues (2019) examined the relative importance of several teacher characteristics for instructional behaviors that have been previously identified as aspects of high quality instruction. Both general (i.e., cognitive ability, personality) and profession-specific teacher characteristics (i.e., enthusiasm for teaching, professional knowledge, beliefs about teaching) were examined in relation to student reports of various instructional practices (i.e., learning support, classroom management, cognitive activation). The results revealed that (teacher-reported) teaching enthusiasm significantly predicted both (student-reported) learning support and classroom management in addition to the significant contributions of personality factors (extraversion, conscientiousness) and pedagogical/psychological knowledge. However, no significant prediction of cognitive activation was observed.
Instructional Practices and Student Outcomes
The studies outlined have included various instructional practices that belong to three broad dimensions of instructional quality: student support, classroom management, and cognitive activation. These dimensions are theorized to represent almost all relevant instructional practices being used by teachers (Klieme et al., 2001, 2009; Praetorius et al., 2018). Importantly, the three general dimensions of instructional quality were found to impact on different student outcomes to varying degrees. For example, cognitively activating teaching tends to affect students' cognitive outcomes such as knowledge, skills, subject understanding, and metacognitive strategy use. In contrast, classroom management and particularly student support are more strongly associated with non-cognitive student outcomes, such as intrinsic motivation, goal orientations, subject matter interest, and well-being (Kunter et al., 2013; Praetorius et al., 2018; Rieser et al., 2016).
Because our focus is on motivational student outcomes (i.e., mastery goals and behavioral engagement), we take a closer look at the support dimension in the following. There are several relevant facets of teacher-provided student support that are likely to impact on student motivation. An important line of research is based on Deci and Ryan’s self-determination theory (Deci & Ryan, 2000; Ryan & Deci, 2002, 2020). According to this theory, instructional practices that are beneficial for students’ intrinsic or self-determined motivation contribute to satisfying students' basic needs for autonomy, competence, and social relatedness. Autonomy supportive teaching is taking place when teachers provide their students with choices and opportunities to work in their own way. Competence support encompasses instructional behaviors that offer optimal challenges to the students and provide effective feedback and freedom from demeaning evaluations. Finally, social relatedness is established if teachers express respect and care for their students and encourage cooperation among their students. Several studies confirm that students who feel supported by their teachers with regard to their basic needs show stronger intrinsic or self-determined motivation to learn (cf. Rakoczy et al., 2008; Theis et al., 2020; for a review, see Ryan & Deci, 2020) and less class-related boredom (Cui et al., 2017). Theis et al. (2020), for example, were able to show that students who perceived support for autonomy, competence, and social relatedness in the classroom also reported stronger mastery goals. Moreover,
Raufelder et al. (2014) found that students reported stronger behavioral engagement when they experienced support for competence and social relatedness (support for autonomy did not attain significance). Finally, Cui et al. (2017) demonstrated a significant indirect effect of student-perceived teacher enthusiasm on class-related boredom mediated by student-perceived autonomy support.
However, there is still a lack of studies relating the above mentioned facets of supportive teaching (i.e., support for autonomy, competence, and social relatedness) to teacher enthusiasm. This is also true for another highly relevant instructional practice that we suggest to be a part of supportive and motivation-inducing instruction, i.e., teaching for meaning in order to increase students’ perception of subject matter relevance. This facet is defined as instructional behavior that aims at making a particular subject matter personally meaningful or relevant to students (Lazarides & Rubach, 2017; Waldis et al., 2002). If a teacher shows a high level of teaching for meaning, then he or she uses, for example, practical examples or presents the teaching material in other ways that are relevant to students’ everyday life. Several studies have demonstrated the motivational effects of supporting subject matter relevance in class (e.g., Gaspard et al., 2020; Hulleman & Harackiewicz, 2009). For example, Lazarides and Rubach (2017) reported significant contributions of student-perceived support for relevance and competence in mathematics classes to students’ mastery goals six months later.
The Present Study
As outlined in the preceding sections, previous research showed that teacher enthusiasm is significantly associated with instructional practices, in particular with practices referring to student support (Kunter et al., 2008, 2011, 2013; Praetorius et al., 2018). Teacher enthusiasm also showed significant relations to students’ motivation and engagement (Frenzel et al., 2019; Patrick et al., 2000; Zhang, 2014). In addition, supportive instructional practices, such as the provision of autonomy, competence, social relatedness, and subject matter relevance, were found to play a crucial role for students’ motivation to learn (Lazarides & Rubach, 2017; Rakoczy et al., 2008; Theis et al., 2020) or class-related emotions (Cui et al., 2017).
Despite these positive findings, there are three noteworthy deficits of previous research: First, with only a few exceptions (e.g., Kunter et al., 2013; Lazarides & Rubach, 2017), most previous studies were cross-sectional. Thus, conclusions regarding longitudinal relations between teacher enthusiasm, instructional practices, and student outcomes are not possible. Second, teacher enthusiasm has only been investigated in relation to a limited range of supportive instructional practices, in particular to learning support. Third, the role of supportive teaching practices as mediators of the relations between teacher enthusiasm and student motivation and engagement has not yet been addressed sufficiently. Although Kunter et al. (2013) examined a mediation model, they focused on students’ enjoyment (an emotional feature) as the dependent variable instead of motivation or engagement.
Based on the outlined shortcomings of previous research on teacher enthusiasm, we conducted a longitudinal study with two measurement points in order to analyze the relations between secondary students’ reports of their mathematics teachers’ enthusiasm and various supportive instructional practices as well as their own motivation and engagement. At the first measurement point, students’ perception of their teachers’ enthusiasm as well as their own motivation (i.e., mastery goal orientation) and behavioral engagement were assessed. At the second measurement point, six months later, students were asked to indicate again their motivation and engagement and to rate their teachers’ supportive instructional practices.
The study refers to the domain of mathematics because it is a core subject in school and of particular importance for students' educational career (Kunter et al., 2011). In addition, mathematical knowledge and skills are increasingly demanded by employers in a wide range of industries (e.g., Hoyles et al., 2002).
The following research questions were addressed: (1) How strong are the predictive contributions of student-perceived teacher enthusiasm to various supportive instructional practices? (2) Is there an indirect relation between teacher enthusiasm and both student motivation and engagement that is mediated by the included facets of student support? In order to examine these questions, students had not only to rate their mastery goals and behavioral engagement but also their teachers’ enthusiasm and four different aspects of teacher-provided support: support for autonomy, competence, social relatedness, and
subject matter relevance (teaching for meaning). Student reports of teachers’ enthusiasm and instructional practices were used because previous findings have shown that students’ perceptions of teacher dispositions and behaviors are more predictive of student outcome variables than teachers’ self-reports (cf. Bieg et al., 2011; Kunter et al., 2008; Schiefele & Schaffner, 2015). Moreover, empirical evidence suggests that student ratings are a reliable and valid source of instructional quality (e.g., Fauth et al., 2014; Wagner et al., 2016). Teachers’ self-ratings of enthusiasm and instructional practices might be biased, for example, by striving to correspond to the ideal image of a teacher (e.g., Kunter & Baumert, 2007). Finally, it should be noted that according to Kunter et al. (2008) students’ ratings of their teachers’ enthusiasm for teaching and for the subject do not form separate factors. Thus, both aspects are part of Kunter et al.’s unidimensional scale of student-perceived teacher enthusiasm that we used in the present study.
Whereas most previous studies focused either on the relations between teacher enthusiasm and instruction or between instruction and student outcomes, we intend to examine the complete pathway from teacher enthusiasm through supportive instructional practices to student motivation and engagement by means of longitudinal data. The full model to be tested is shown in Figure 1. Notably, Time 1 measures of student outcome variables were included in the model in order to control for differences in initial levels of these variables. This permits more appropriate interpretations of possibly observed associations between instructional practices and both student motivation and engagement.
Figure 1 Theoretical Model
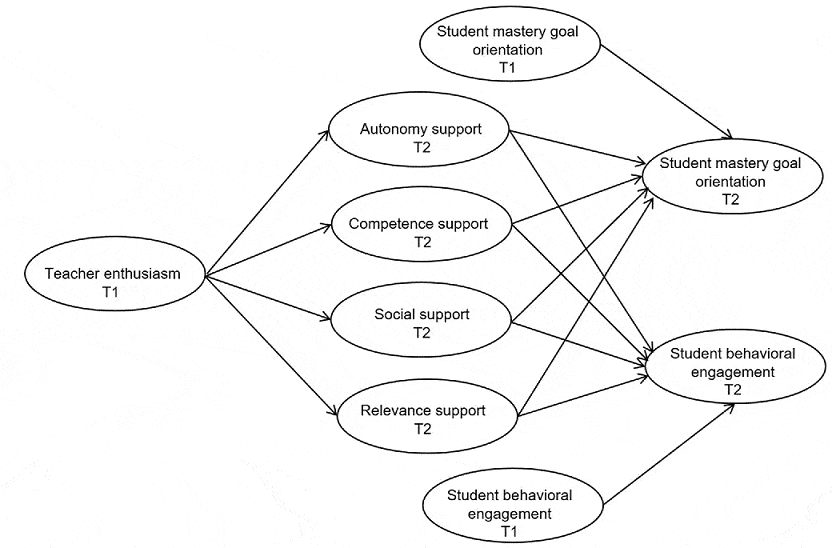
Note. T1= Time 1; T2 = Time 2.
As is depicted in the model in Figure 1, we hypothesized that student-reported teacher enthusiasm at the beginning of the school year positively predicts student-perceived supportive instructional practices (i.e., support for autonomy, competence, social relatedness, and subject matter relevance) in the middle of the school year. In line with previous findings (Kunter et al., 2008, 2011, 2013; Lazarides et al., 2018), we assume that teachers’ enthusiasm for their subject and for teaching likely leads them to support their students’ feelings of autonomy, competence, and social relatedness. Moreover, enthusiastic teachers presumably are able to evoke their students’ belief in mathematics as something personally meaningful or relevant.
In addition to the effects of teacher enthusiasm on supportive instructional practices, we hypothesized that student reports of teacher-provided support contribute to students' mastery goal orientation and behavioral engagement in mathematics. As described earlier, this assumption is backed by both theory (e.g., Ryan & Deci, 2020; Urdan & Schoenfelder, 2006) and empirical evidence (e.g., Hulleman & Harackiewicz, 2009; Theis et al., 2020).
Finally, as implied by our hypothetical model in Figure 1, we did not assume direct relations between teacher enthusiasm and student mastery goals and engagement. Instead, we expected only indirect relations between teacher enthusiasm and student outcomes that are mediated by all four supportive instructional practices. Thus, we suggest that teachers’ enthusiasm has only effects on students if it is transformed into appropriate instructional practices. Preliminary evidence provided by Kunter et al. (2008, 2011, 2013) and Lazarides and Rubach (2017) supports our suggestion.
Method
Participants and Procedure
The student sample (n = 751) comprised 404 9th (53.8%) and 346 10th graders (46.1%; n = 1 missing indication of grade). Somewhat more than half of the sample was female (56.0%, n = 12 missing indications of gender) and the average age was 14.50 (SD = 0.85; range: 12-19; n = 14 missing indications of age). Students came from 46 classrooms (average class size: 16.3 students) in 11 secondary schools located in a large city in Germany. A majority of students reported that they were native German speakers (70.2%, n = 27 missing indications of mother tongue). At Time 1, about half of the students attended a gymnasium (the academic track in Germany; 53.3 %, n = 13 missing indication of school type). The other half of the students (45.0%) attended an integrated secondary school where students attend different courses depending on their achievement levels. Only data from students who participated at both Time 1 and 2 were included in the present analyses. At Time 1, a total of 1117 students participated in the study.
In order to examine whether the group of students who dropped out after Time 1 (n = 366) differed significantly from the current sample of 751 students, we compared the mean values of all study variables (teacher enthusiasm; support for autonomy, competence, social support, and subject matter relevance; students’ mastery goals and behavioral engagement) between the two groups by means of two-tailed t–tests. These tests yielded significant (p < .01) moderate differences only for perceived support for competence (d = 0.52) and social relatedness (d = 0.59), with lower means for the dropout sample.
The first wave of data collection was conducted about two months after the start of the school year. The second wave followed about six months after the first wave in the middle of the school year. Questionnaires were administered by trained research assistants and took about 30 minutes to complete. Students were informed about the voluntary nature of their participation. Parental consent was obtained for students below the age of 14.
Measures
All questionnaire items had to be rated on five-point rating scales indicating either agreement (ranging from 1 [do not agree at all] to 5 [agree completely]) or frequency (ranging from 1[never] to 5 [nearly always]). For all scales, higher scores represent higher levels in the specific construct. Descriptive statistics and reliabilities (Cronbachs’ alpha) for all variables are reported in Table 1.
Table 1 Means, Standard Deviations, and Reliability Coefficients for all Variables
Variable |
n |
M |
SD |
α |
ICC(1) |
ICC(2) |
Teacher enthusiasm T1 |
715 |
3.49 |
1.08 |
.86 |
.30 |
.88 |
Autonomy support T2 |
744 |
2.82 | 0.94 |
.77 |
.14 |
.72 |
Competence support T2 |
744 |
3.30 |
1.00 |
.81 |
.12 |
.68 |
Social support T2 |
743 |
3.70 |
0.91 |
.76 |
.06 |
.52 |
Relevance support T2 |
737 |
3.20 |
1.01 |
.86 |
.27 |
.86 |
Mastery goals T1 |
746 |
3.13 |
1.00 |
.82 |
.07 |
.55 |
Mastery goals T2 |
748 |
3.13 |
0.97 |
.82 |
.05 |
.48 |
Behavioral engagement T1 |
734 |
3.37 |
0.92 |
.82 |
.08 |
.57 |
Behavioral engagement T2 |
744 |
3.38 |
0.91 |
.84 |
.05 |
.45 |
Note. T1 = Time 1; T2 = Time 2.
Student-Perceived Teacher Enthusiasm: To capture students’ perceptions of their mathematics teachers' enthusiasm, a three-item scale developed by Kunter et al. (2008) was used. Students were asked to indicate their degree of agreement with the following statements: “Our mathematics teacher seems to really enjoy teaching”, “Our mathematics teacher is an enthusiastic teacher”, and “Our mathematics teacher is enthusiastic about the subject of mathematics”. Thus, this scale refers to both teachers’ enthusiasm for teaching
and for the subject. Based on the results of a confirmatory factor analysis, Kunter et al. confirmed the unidimensional structure of their scale. Consequently, it can be concluded that students do not differentiate between the two facets of teacher enthusiasm when they perceive their teachers’ behavior in the classroom.
Student-Perceived Support: Students’ perceptions of their teachers’ support for autonomy, competence, and social relatedness were measured by means of three-item scales developed by Rakoczy (2006). In this case, students had to indicate frequencies referring to certain events or teacher behaviors in the classroom. The opening stem for all items was “In our mathematics class, …”, followed by these items: “… I have the opportunity to explore new topics on my own”, “… I have the opportunity for in-depth study of interesting tasks or contents”, and “… I can decide for myself how I want to work” (autonomy support), “… the teacher tells me how I could improve”, “… my achievements are acknowledged”, and “… I am praised for good performance” (competence support), “… I feel as if I would belong”, “… I feel as if the other students would help me if necessary” and “… I feel understood by the other students” (social support).
The extent to which students perceived their teachers as making the material in mathematics lessons meaningful or relevant to them was assessed by means of a three-item scale, which was created by Waldis et al. (2002) and adapted by Klieme and Reusser (2003). Students were asked to indicate their agreement with these statements: “Our mathematics teacher often gives us practical examples which help us to discover mathematical rules”, “When we elaborate something new in mathematics, we usually draw on our own experiences and everyday examples”, and “To explain something mathematical to us, our mathematics teacher often uses practical examples from everyday life”.
Students’ Self-Reported Mastery Goal Orientation: We translated a scale developed by Midgley et al. (2000) into German in order to assess students’ mastery goal orientation. Students had to estimate their agreement with these items (opening stem: “I like class work in mathematics class…”): “…when it really makes me think”, “… when I work intensively”, and “…when the tasks require me to think hard”.
Students’ Self-Reported Behavioral Engagement: In order to measure behavioral engagement, we used a translated and adapted version of a scale proposed by Elliot (1997). This scale focuses on students’ effort and persistence when working on mathematical tasks. Specifically, students had to rate their agreement with these four statements: “If I have difficulties with a task in mathematics, I repeat it to practice”, “If mathematical tasks that I calculate are difficult, I practice them extra until I can do them really well”, “I try to learn and perform well, even if a task is boring”, and “I work hard in mathematics to do well even if I don’t like what we are doing”.
Statistical Analyses
Because of the hierarchical data structure in the present study, wherein students were nested in 46 classes, we computed intra-class correlation coefficients, ICC(1) and ICC(2), to examine whether class-level aggregation of the constructs was justified (see Table 1). ICC(1) indicates the proportion of explained variance in individual student ratings by class membership. ICC(2) informs about the reliability of the aggregated class means (e.g., Bliese, 2000). The ICC(2) is calculated by applying the Spearman-Brown formula (Bliese, 2000), taking into account the ICC(1) and the average class size. As a rule of thumb, it has been suggested that ICC(1) values of at least 5% of explained variance and ICC(2) values of at least .70 are required for justifying the aggregation of individual scores (e.g., LeBreton & Senter, 2008; Lüdtke & Trautwein, 2007). The findings revealed that only four out of nine coefficients showed satisfactory values for ICC(1) and ICC(2). In particular, the dependent variables (students’ mastery goal orientation and behavioral engagement) exhibited rather low between class variations (see Table 1). Therefore, it seemed not appropriate to conduct class-level analyses based on aggregated student ratings. We, thus, decided to perform all statistical analyses only at the individual student level.
In order to test the model specified in Figure 1, structural equation analyses with latent variables were conducted by means of the statistical software Mplus version 8.0 (Muthén & Muthén, 1998-2017a). All latent variables were specified at the item level. Moreover, structural equation analyses were performed by using the MLR estimator (Maximum Likelihood parameter estimator with Robust standard errors). MLR estimates standard errors and chi-square statistics that are robust to non-normality and non-independence of observations when used with the TYPE=COMPLEX option (Muthén & Muthén, 1998-2017b). The TYPE=COMPLEX option was applied in order to account for the hierarchical data structure and the resulting non-independence of individual scores (LeBreton & Senter, 2008; Muthén & Muthén, 1998-2017b). Indirect effects were tested by means of the delta method (MacKinnon, 2008, p. 92), which is the default test in Mplus. Goodness of model fit was evaluated by the following criteria (Hu & Bentler, 1999; Tanaka, 1993): Tucker-Lewis index (TLI), comparative fit index (CFI), root mean square error of approximation (RMSEA), and standardized root mean square residual (SRMR). An acceptable fit can be concluded for values of TLI and CFI greater than or equal to .90, RMSEA below or equal to .08, and SRMR below or equal to .10. A good fit is indicated by values of TLI and CFI greater than or equal to .95, RMSEA below or equal to .06, and SRMR below or equal to .08 (cf. Hu & Bentler, 1999).
In the present study, only a small amount of missing data occurred (M = 1.5%; Range: 0.4 – 4.8%, see varying sample size in Table 1). We applied Little’s Missing Completely at Random (MCAR) test (cf. Little & Rubin, 2002) and found no indication of a systematic accumulation of missing data patterns in the dependent variables (mastery goals and behavioral engagement at Time 2) and control variables (mastery goals and behavioral engagement at Time 1) when considering student gender, χ2 (29) = 18.025, p = .944. In the structural equation models, missing data were treated by applying the full-information maximum likelihood (FIML) algorithm.
Result
Descriptive Statistics and Bivariate Correlations
Manifest mean values, standard deviations, and reliability coefficients for all variables are reported in Table 1. Overall, the results show moderately positive values for students’ evaluation of their teachers’ enthusiasm and instructional practices. The bivariate correlations among the study variables were low or moderate and in accordance with our hypotheses (see Table 2). In particular, significant correlations between teacher enthusiasm and the instruction variables were observed. The correlational analyses also indicated significant relations between teacher enthusiasm and students’ mastery goals and behavioral engagement. Moreover, all four instruction variables were significantly associated with each other and with the measures of students’ mastery goals and behavioral engagement at Time 2.
Table 2 Manifest Bivariate Correlations Among All Variables
Variable |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
1. Student gendera |
- |
|
|
|
|
|
|
|
|
|
|
2. Student grade T1b |
-.05 |
- |
|
|
|
|
|
|
|
|
|
3. School typec |
-.14*** |
.19*** |
- |
|
|
|
|
|
|
|
|
4. Teacher enthusiasm T1 |
-.01 |
-.07 |
.01 |
- |
|
|
|
|
|
|
|
5. Autonomy support T2 |
-.08* |
-.01 |
-.01 |
.16*** |
- |
|
|
|
|
|
|
6. Competence support T2 |
-.09* |
-.01 |
.15*** |
.33*** |
.41*** |
- |
|
|
|
|
|
7. Social support T2 |
-.01 |
-.00 |
-.10** |
.13*** |
.24*** |
.40*** |
- |
|
|
|
|
8. Relevance support T2 |
-.04 |
-.03 |
.07 |
.36*** |
.42*** |
.48*** |
.19*** |
- |
|
|
|
9. Mastery goals T1 |
-.10** |
-.05 |
-.04 |
.20*** |
.17*** |
.18*** |
.15*** |
.18*** |
- |
|
|
10. Mastery goals T2 |
-.05 |
-.09** |
-.03 |
.19*** |
.30*** |
.31*** |
.30*** |
.30*** |
.51*** |
- |
|
11. Behavioral engagement T1 |
.07* |
-.06 |
-.06 |
.24*** |
.13*** |
.18*** |
.22*** |
.16*** |
.43*** |
.33*** |
- |
12. Behavioral engagement T2 |
.07 |
-.08* |
-.05 |
.15*** |
.22*** |
.26*** |
.27*** |
.23*** |
.23*** |
.42*** |
.51*** |
Note. 701 < n < 750 (pairwise missings). T1 = Time 1; T2 = Time 2. aScoring of gender: male = 1, female = 2.bScoring of grade level: 9th grade = 1, 10th grade = 2. cScoring of school type: 1 = gymnasium, 2 = integrated secondary school. * p < .05, two-tailed. ** p < .01, two-tailed. *** p < .001, two-tailed.
With regard to gender, grade level, and school type mostly non-significant and low correlations were obtained. However, we observed a significant but weak tendency for male students to perceive stronger support for autonomy and competence, and to be more mastery goal oriented at Time 1 than female students. These findings are in line with previous studies involving gender differences pertaining to mathematics (Lazarides & Watt, 2015; Nagy et al., 2006). Moreover, there were low but significant correlations between students’ grade level and both students’ mastery goals and behavioral engagement at Time 2. Accordingly, 9th graders reported slightly higher values than 10th graders at Time 2.
The findings referring to school type indicate that more girls than boys attended the gymnasium (which is representative for Germany and many other countries; Neugebauer, 2011) and students felt more support for competence and less support for social needs at the integrated secondary schools compared to the gymnasium. The latter finding is likely to be due to the fact that students in secondary schools show lower achievement levels than students in the gymnasium. Thus, secondary school teachers may focus more strongly on fostering their students’ competence, at the expense of providing social relatedness.
Finally, the significant association between school type and grade level indicates that the classes from integrated secondary schools were at a somewhat higher grade level on average than the classes from gymnasium schools.
Structural Equation Analyses
As a first step in the analysis of the hypothesized mediation model (see Figure 1), we tested the measurement part of the model, that is, without specifying the assumed structural paths. The results showed an acceptable fit, χ² = 1144.118, df = 341, p < .001, CFI = .91, TLI = .89, RMSEA = .06, SRMR = .05. However, modification indices suggested a substantial improvement of the model by including correlations between error terms of the following items: behavioral engagement items 1 and 2 (“If I have difficulties with a task in mathematics, I repeat it to practice”; “If mathematical tasks that I calculate are difficult, I practice them extra until I can do them really well”), 3 and 4 (“I try to learn and perform well, even if a task is boring”; “I work hard in mathematics to do well even if I don’t like what we are doing”), and competence support items 3 and 4 (“In our mathematics class, my achievements are acknowledged”; “In our mathematics class, I am praised for good performance”). These correlations between error terms were most likely caused by shared content and therefore theoretically justified (cf. Kline, 2016). The adapted measurement model showed a good fit with the empirical data, χ² = 632,127, df = 336, p < .001, CFI = .97, TLI = .96, RMSEA = .03, SRMR = .04. Each latent construct was adequately represented by the items used, as indicated by the significant standardized factor loadings, which all exceeded the value of .50.
As a second step, the assumed structural paths were added to the model. In line with our hypotheses, only indirect paths between student-perceived teacher enthusiasm and student motivation were assumed. Moreover, we included gender, grade level, and school type as additional control variables by specifying structural paths from these variables to all T2 variables in the model.
Table 3 Bidirectional Paths in the Structural Equation Model
Variable |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
1. Teacher enthusiasm T1 |
- |
|
|
|
|
|
|
|
2. Autonomy support T2 |
|
- |
|
|
|
|
|
|
3. Competence support T2 |
|
.58*** |
- |
|
|
|
|
|
4. Social support T2 |
|
.32*** |
.51*** |
|
|
|
|
|
5. Relevance support T2 |
|
.48*** |
.56*** |
.22*** |
- |
|
|
|
6. Mastery goals T1 |
.24*** |
|
|
|
|
- |
|
|
7. Behavioral engagement T1 |
.27*** |
|
|
|
|
.52*** |
- |
|
8. Mastery goals T2 |
|
|
|
|
|
|
|
- |
9. Behavioral engagement T2 |
|
|
|
|
|
|
|
.40*** |
Note. Statistics are standardized regression coefficients. T1 = Time 1; T2 = Time 2. ***p < .001
The fit of the structural model remained almost at the level of the measurement model, thus indicating a good fit, χ² = 841.07, df = 417, p < .001, CFI = .95, TLI = .94, RMSEA = .04, SRMR = .06. The resulting model in Figure 2 only shows the assumed unidirectional paths. The specified bidirectional paths are presented in Table 3. As expected, we obtained significant moderate or high associations among the four instruction variables, between teacher enthusiasm and the Time 1 control variables (mastery goals and engagement), and between mastery goals and engagement at both Time 1 and 2. The additional control variables (gender, grade level, school type) were not significantly related to the T2 variables in the model, with only two exceptions: A lower grade level was associated with higher mastery goals (β = -.08, p < .05) and attending an integrated secondary school was related to higher perceptions of competence support (β = .17, p = .001).
Figure 2 Structural Equation Model of the Relations Between Teacher Enthusiasm, Instructional Practices, and Student Engagement and Motivation
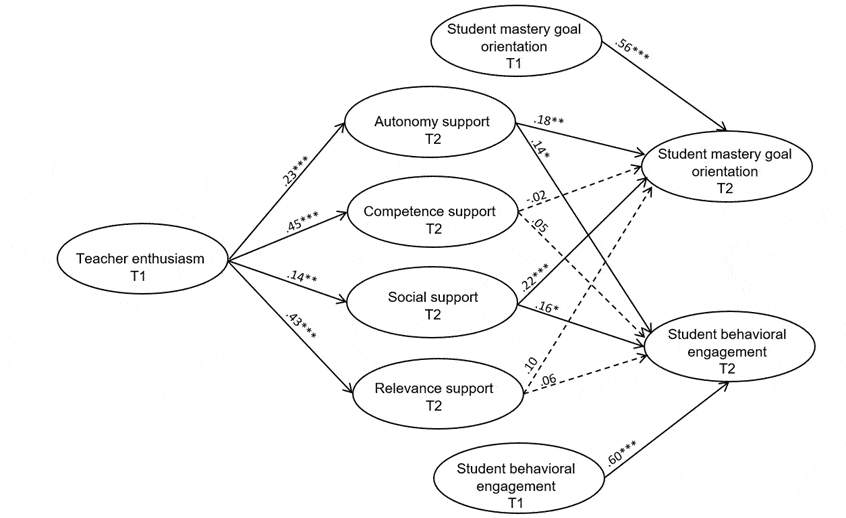
Note. Statistics are standardized regression coefficients. For the sake of clarity, correlational paths (see Table 3) and the effects of additional control variables (gender, grade level, school type) are not depicted here. Dotted lines represent non-significant relations. T1= Time 1; T2 = Time 2. * p < .05. **p < .01. ***p < .001.
As is depicted in Figure 2, students who perceived their teachers as enthusiastic at Time 1 reported higher provision of support for autonomy, competence, social relatedness, and subject matter relevance six months later. Moreover, both students’ mastery goals and behavioral engagement at Time 2 were significantly associated only with support for autonomy and social relatedness. Importantly, these relations were observed while controlling for Time 1 levels of the dependent variables.
The analyses revealed significant total indirect effects of teacher enthusiasm on students’ mastery goals (β = .11, p < .001, 95% CI [.05, .17]) and behavioral engagement (β = .10, p < .001, 95% CI [.05, .15]). However, specific indirect effects attained significance only for autonomy support (β = .04, p < .05, 95% CI [.01, .07]) and social support (β = .03, p = .01, 95% CI [.01, .05] as mediators of the indirect relation between teacher enthusiasm on students’ mastery goals.
Although mediation analyses do not necessarily presuppose significant direct effects between predictor and outcome variables (cf. Shrout & Bolger, 2002), it is noteworthy that we observed such direct effects as indicated by significant manifest (see Table 2) and latent correlations between teacher enthusiasm and students’ mastery goals (rlatent = .21, p < .001) as well as behavioral engagement (rlatent = .17, p < .01). In addition, when entering direct paths from teacher enthusiasm to the dependent variables in our model, significant positive direct effects were not obtained.
Discussion
In extending previous research, the present study examined a longitudinal indirect effects model that hypothesized significant relations of teacher enthusiasm to various supportive instructional practices (i.e., support for autonomy, competence, social relatedness, and subject matter relevance), which in turn were assumed to be related to students’ mastery goal orientation and behavioral engagement in mathematics. Thus, only indirect effects of teacher enthusiasm on students’ motivation and engagement were proposed. The model was at least partially confirmed. First, students who rated their teachers as more enthusiastic at the beginning of the school year perceived stronger support for their basic needs for autonomy, competence, and social relatedness six months later. In addition, students with more enthusiastic teachers reported higher levels of support for subject matter relevance, for example, by providing practical examples and drawing connections to students’ everyday life. These findings confirm the positive effects of teacher enthusiasm on instructional quality that have been reported by previous studies (e.g., Cui et al., 2017; Kunter et al., 2008, 2011, 2013; Lazarides et al., 2018).
Second, we observed that autonomy support and social support, but not support for competence and relevance, were related to both student mastery goals and engagement. These findings contrast with our expectation that all four supportive practices might be relevant for student mastery goals and engagement. Instead, the present results clearly suggest that social support and autonomy support are more important for students’ mastery goals and behavioral engagement in mathematics than support for competence and relevance. Interestingly, this pattern of findings deviates from the analysis of bivariate manifest correlations (see Table 2) which yielded rather similar associations between the four instruction variables and students’ mastery goals and behavioral engagement. The relative predictive weights of the instruction variables became evident only when including these variables simultaneously in our model.
A closer look at the present measures of mastery goals and engagement can help to explain the specific pattern of relations observed in our model. The scale of student mastery goals is about liking class work when it is challenging and engaging (e.g., “I like class work in mathematics class when it really makes me think”). Thus, mastery goal-oriented students do not feel pressured to work on (difficult or boring) tasks but like to be challenged by and involved in interesting class work. The measure of student engagement scale emphasizes effort and persistence in a learning activity, even if tasks are difficult or unpopular (e.g., “If mathematical tasks that I calculate are difficult, I practice them extra until I can do them really well”). It seems plausible that in particular students’ mastery goal orientation is fostered by providing them with the space and choices to take ownership, take initiative, and causal agency (cf. Ryan & Deci, 2002, 2020). In the same way, students whose learning activities are characterized by great effort and persistence seem to benefit from autonomy-supporting and non-controlling instructional behaviors of the teacher. Numerous studies have already confirmed the positive relations between autonomy supportive teaching and student motivation (e.g., Bieg et al., 2011; Black & Deci, 2000; Theis et al., 2020; for a review, see Ryan & Deci, 2020). Moreover, students seem to take advantage of the scope for autonomy when they feel related in an authentic and caring way to their teacher and their classmates (Reeve, 2012). In fact, the intertwined effects of autonomy support and experienced social relatedness have been explained by assuming that autonomy-supportive teachers are more likely to take students’ perspective and are more responsive to their concerns (cf. Ryan & Deci, 2020).
How can we explain the missing contributions of competence and relevance support to student motivation and engagement? As described above, the dependent variables in question (mastery goals and engagement) are likely to benefit, due to their very nature, most strongly when students feel autonomous and socially related. In the case of relevance perceptions, the failure to find significant effects could be additionally explained by the fact that relevance instructions have been proven particularly important for subject matter interest and intrinsic motivation to learn (cf. Bergin, 2016).
However, from a theoretical perspective, feelings of competence seem also likely to facilitate mastery goals and engagement. The lack of this effect could be due to the fact that autonomy support also impacts on competence perceptions. Indeed, several studies have indicated that autonomy-supported students tend to perceive an increase in their competence and self-esteem (e.g., Black & Deci, 2000; Deci et al., 1981). Moreover, it is important to note that in the model we controlled for initial levels of motivation and engagement. Consequently, the dependent variables in the model represent changes from Time 1 to Time 2. Thus, it seems possible that while competence support is positively associated with student mastery goals and engagement, an increase in these variables depends more strongly on students’ experience of autonomy and social relatedness. In addition, it should be noted that competence support in the present study was mainly covered by the aspect of teacher praise or recognition, whereas the aspect of constructive or informative feedback was not included. This leads to the conclusion that student-perceived teacher praise or recognition does not contribute to an increase in students’ mastery goals and engagement whereas a more constructive or informative feedback would lead to higher student motivation (cf. Kiemer et al., 2015). In addition, it can be argued that students who receive praise or recognition from their teacher also feel more socially related in their class (cf., Brophy, 1981, Skipper & Douglas, 2015). Thus, the effects of competence support and social support might have been confounded in the present study.
In extending previous research (e.g., Butler, 2012; Kunter et al., 2013; Lazarides et al., 2017; Schiefele, 2017), we were able to confirm indirect relations between student-perceived teacher enthusiasm and both student mastery goals and engagement that are mediated by supportive instructional practices. While we found significant total indirect effects of teacher enthusiasm on student mastery goals and engagement, it is important to note that only autonomy and social support were significantly related to the dependent variables. Accordingly, specific indirect effects of teacher enthusiasm on student mastery goals were only obtained for autonomy and social support. However, specific indirect effects of teacher enthusiasm on student engagement did not attain significance, although the significant total indirect effect in this case also relies mainly on the mediation effects of both autonomy and social support.
Limitations, Future Research, and Conclusions
There are at least two limitations that need to be addressed by future research. First, the present study focused on a particular subject (mathematics) and grade level (9th and 10th grade students). There is in particular considerable agreement that the effects of instructional practices on student outcomes are subject-specific (Baumert et al., 2010; Wagner et al., 2013). Thus, the present results cannot readily generalized to other subjects or grade levels. It seems therefore desirable for future research to investigate subject areas other than mathematics and refer to both lower and higher grade levels than those in the present study.
Second, the present study comprised only two measurement points. Instructional practices as well as student motivation and engagement were assessed at the same time. Consequently, the association between instructional practices and student outcomes is likely to be overestimated by the present data. Therefore, future studies are advised to conduct three waves of measurement and assess all three groups of variables – teacher motivations, instructional practices, and student outcomes – at each wave. This would also allow to examine the reciprocity of the relations between teacher motivation, instructional practices, and student outcomes. Such relations are to be expected as recent studies observed reciprocal effects between teacher self-efficacy and instructional quality (Holzberger et al., 2013) and between teacher enthusiasm and various student variables such as achievement and enjoyment (Kunter et al., 2011).
Third, it seems worthwhile to include also teacher self-reports of enthusiasm in order to examine longitudinal reciprocal effects between teacher enthusiasm and student motivation. For instance, Frenzel et al. (2018) found evidence for a reciprocal transmission of enjoyment in class between teachers and students. Similar processes could occur between teacher and student motivation.
Fourth, future research on teacher enthusiasm and instructional quality should include not only student measures of motivation but also of achievement (e.g., Moè, 2016; Moè et al., 2020). It seems likely that different aspects of instructional quality are relevant for student motivation vs. achievement. For example, competence support is likely to be closely and reciprocally associated with academic achievement, whereas social support might be less relevant in this case.
We understand the present study as part of a larger effort to investigate the specific relations between teacher motivations, instructional practices, and student outcomes more deeply (cf. Lazarides & Schiefele, in press). As a possible result of this effort, more knowledge could be provided about which teacher motivations affect which practices in the classroom, and which practices are related to which student outcomes.
Such knowledge would be highly important for teacher education as it would allow specifying the teacher motivations and practices that are most important for student motivation, engagement, and achievement. As a first step to provide knowledge on the differential relations between teacher and student variables, the present study suggests that teacher enthusiasm appears as an important teacher characteristic that unfolds its effects on student motivation and engagement by means of supportive instructional practices (support for autonomy, competence, social relatedness, and subject matter relevance). A particularly interesting result pertains to the specificity of relations between instructional practices and student outcomes. Our findings suggest that students’ mastery goals and behavioral engagement are strongly associated with both student-perceived autonomy and social support, but not with competence or relevance support. In addition, autonomy and social support seem to play an important role as mediators of the indirect effects of teacher enthusiasm on student mastery goals and engagement.
It is noteworthy that enthusiasm might be also beneficial for the teachers themselves. For example, several studies found positive relations between teacher enthusiasm and self-efficacy, job satisfaction, and lower risk for burnout (e.g., Buric & Moè, 2020; Taxer & Frenzel, 2018). These factors, in turn, are related to the greater tendency of teachers to support the needs of their students (e.g., Moè & Katz, 2020; Opdenakker & van Damme, 2006).
Given the importance of teacher enthusiasm for both students and teachers, we suggest that teacher training should pay special attention to fostering interest and enjoyment in teaching and the subject. Moreover, in the day-to-day work of teachers, an environment is needed that allows for maintaining enthusiasm. This includes, for example, avoiding stressful working conditions such as the increased burden of administrative and management tasks teachers are required to do. Ultimately, by promoting teacher enthusiasm, a sustainable positive effect on teaching quality, teacher well-being and, consequently, on student motivation, engagement, and learning can be achieved.
Acknowledgement
We would like to thank Dr. Charlott Rubach for her extensive contributions to organizing the study and collecting the data.
References
- Archambault, I., Janosz, M., Fallu, J., & Pagani, L. S. (2009). Student engagement and its relationships with early high school dropout. Journal of Adolescence, 32, 651–670. https://doi.org/10.1016/j.adolescence.2008.06.007
- Baier, F., Decker, A. T., Voss, T., Kleickmann, T., Klusmann, U., & Kunter, M. (2019). What makes a good teacher? The relative importance of mathematics teachers' cognitive ability, personality, knowledge, beliefs, and motivation for instructional quality. British Journal of Educational Psychology, 89(4), 767–786. https://doi.org/10.1111/bjep.12256
- Barron, K. E., & Harackiewicz, J. M. (2001). Achievement goals and optimal motivation: Testing multiple goal models. Journal of Personality and Social Psychology, 80(5), 706–722. https://doi.org/10.1037/0022-3514.80.5.706
- Baumert, J., Kunter, M., Blum, W., Brunner, M., Voss, T., Jordan, A., Klusmann, U., Krauss, S., Neubrand, M., & Tsai, Y.-M. (2010). Teachers’ mathematical knowledge, cognitive activation in the classroom, and student progress. American Educational Research Journal, 47(1), 133–180. https://doi.org/10.3102/0002831209345157
- Bergin, D. A. (2016). Social influences on interest. Educational Psychologist, 51(1), 7-22. https://doi.org/10.1080/00461520.2015.1133306
- Bieg, S., Backes, S., & Mittag, W. (2011). The role of intrinsic motivation for teaching, teachers' care and autonomy support in students' self-determined motivation. Journal of Educational Research Online, 3(1), 122-140.
- Black, A. E., & Deci, E. L. (2000). The effects of instructors’ autonomy support and students’ autonomous motivation on learning organic chemistry: A self-determination theory perspective. Science Education, 84(6), 740–756. https://doi.org/10.1002/1098-237X(200011) 84:6<740::AID-SCE4>3.0.CO;2-3
- Bliese, P. D. (2000). Within-group agreement, non-independence, and reliability: Implications for data aggregation and analysis . In K. J. Klein & S. W. Kozlowski (Eds.), Multilevel theory, research, and methods in organizations (pp. 349–381). Jossey-Bass.
- Brophy, J. (1981). Teacher praise: A functional analysis. Review of Educational Research, 51(1), 5-32. https://doi.org/10.3102/00346543051001005
- Burić, I., & Moè, A. (2020). What makes teachers enthusiastic: The interplay of positive affect, self-efficacy and job satisfaction. Teaching and Teacher Education, 89(7), 103008. https://doi.org/10.1016/j.tate.2019.103008
- Butler, R. (2006). Are mastery and ability goals both adaptive? Evaluation, initial goal construction and the quality of task engagement. British Journal of Educational Psychology, 76, 595-611. https://doi.org/10.1348/000709905X52319
- Butler, R. (2012). Striving to connect: Extending an achievement goal approach to teacher motivation to include relational goals for teaching. Journal of Educational Psychology, 104(3), 726–742. https://doi.org/10.1037/a0028613
- Butler, R., & Shibaz, L. (2014). Striving to connect and striving to learn: Influences of relational and mastery goals for teaching on teacher behaviors and student interest and help seeking . International Journal of Educational Research, 65, 41–53. https://doi.org/10.1016/j.ijer.2013.09.006
- Cui, G., Yao, M., & Zhang, X. (2017). The dampening effects of perceived teacher enthusiasm on class-related boredom: The mediating role of perceived autonomy support and task value. Frontiers in Psychology, 8 , 400. https://doi.org/10.3389/fpsyg.2017.00400
- Deci, E. L., & Ryan, R. M. (2000). The "what" and "why" of goal pursuits: Human needs and the self-determination of behavior. Psychological Inquiry, 11(4), 227–268. https://doi.org/10.1207/S15327965PLI1104_01
- Deci, E. L., Schwartz, A. J., Sheinman, L., & Ryan, R. M. (1981). An instrument to assess adults' orientations toward control versus autonomy with children: Reflections on intrinsic motivation and perceived competence. Journal of Educational Psychology, 73(5), 642–650. https://doi.org/10.1037/0022-0663.73.5.642
- Elliot, A. J. (1997). Integrating the “classic” and “contemporary” approaches to achievement motivation: A hierarchical model of approach and avoidance achievement motivation . In M. Maehr & P. Pintrich (Eds.), Advances in motivation and achievement (Vol. 10, pp. 243–279). JAI Press.
- Fauth, B., Decristan, J., Rieser, S., Klieme, E., & Büttner, G. (2014). Student ratings of teaching quality in primary school: Dimensions and prediction of student outcomes. Learning and Instruction, 29, 1–9. https://doi.org/10.1016/j.learninstruc.2013.07.001
- Fauth, B., Decristan, J., Decker, A.‑T., Büttner, G., Hardy, I., Klieme, E., & Kunter, M. (2019). The effects of teacher competence on student outcomes in elementary science education: The mediating role of teaching quality. Teaching and Teacher Education, 86, 102882. https://doi.org/10.1016/j.tate.2019.102882
- Frenzel, A. C., Becker-Kurz, B., Pekrun, R., Goetz, T., & Lüdtke, O. (2018). Emotion transmission in the classroom revisited: A reciprocal effects model of teacher and student enjoyment. Journal of Educational Psychology, 110(5), 628–639. https://doi.org/10.1037/edu0000228
- Frenzel, A. C., Goetz, T., Lüdtke, O., Pekrun, R., & Sutton, R. E. (2009). Emotional transmission in the classroom: Exploring the relationship between teacher and student enjoyment. Journal of Educational Psychology, 101(3), 705–716. https://doi.org/10.1037/a0014695
- Frenzel, A. C., Taxer, J. L., Schwab, C., & Kuhbandner, C. (2019). Independent and joint effects of teacher enthusiasm and motivation on student motivation and experiences: A field experiment. Motivation and Emotion, 43(2), 255–265. https://doi.org/10.1007/s11031-018-9738-7
- Gaspard, H., Parrisius, C., Piesch, H., Kleinhansl, M., Wille, E., Nagengast, B., Trautwein, U., & Hulleman, C. S. (2020). The potential of relevance interventions for scaling up: A cluster-randomized trial testing the effectiveness of a relevance intervention in math classrooms. PsyArXiv. https://doi.org/10.31234/osf.io/ahj3m
- Guan, J., Xiang, P., McBride, R., & Bruene, A. (2006). Achievement goals, social goals, and students’ reported persistence and effort in high school physical education. Journal of Teaching in Physical Education, 25, 58-74. https://doi.org/10.1123/jtpe.25.1.58
- Harackiewicz, J. M., Barron, K. E., Trauer, J. M., Carter, S., & Elliot, A. J. (2000). Short-term and long-term consequences of achievement goals: Predicting interest and performance over time. Journal of Research in Science Teaching, 92(2), 316–330. https://doi.org/10.1037/0022-0663.92.2.316
- Holzberger, D., Philipp, A., & Kunter, M. (2013). How teachers’ self-efficacy is related to instructional quality: A longitudinal analysis. Journal of Educational Psychology, 105(3), 774–786. https://doi.org/10.1037/a0032198
- Hoyles, C., Wolf, A., Molyneux-Hodgson, S., & Kent, P. (2002). Mathematical skills in the workplace: Final report to the Science Technology and Mathematics Council. I nstitute of Education, University of London. https://discovery.ucl.ac.uk/id/eprint/1515581/1/Hoyles2002MathematicalSkills.pdf
- Hu, L.‐T., & Bentler, P. M. (1999). Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Structural Equation Modeling: A Multidisciplinary Journal, 6(1), 1–55. https://doi.org/10.1080/10705519909540118
- Hulleman, C. S., & Harackiewicz, J. M. (2009). Promoting interest and performance in high school science classes. Science, 326(5958), 1410-1412. https://doi.org/10.1126/science.1177067
- Keller, M. M., Hoy, A. W., Goetz, T., & Frenzel, A. C. (2016). Teacher enthusiasm: Reviewing and redefining a complex construct. Educational Psychology Review, 28(4), 743–769. https://doi.org/10.1007/s10648-015-9354-y
- Keller, M. M., Neumann, K., & Fischer, H. E., (2014). Enthusiastic teaching and its impact on students’ interest and self-concept: An investigation of German physics classrooms . In H. E. Fischer, P. Labudde, K. Neumann, & J. Viiri (Eds.), Quality of instruction in physics-comparing Finland, Germany and Switzerland (pp. 129-144). Waxmann.
- Kiemer, K., Gröschner, A., Pehmer, A.-K., & Seidel, T. (2015). Effects of a classroom discourse intervention on teachers' practice and students' motivation to learn mathematics and science . Learning and Instruction, 35, 94–103. https://doi.org/10.1016/j.learninstruc.2014.10.003
- Klieme, E., Pauli, C., & Reusser, K. (2009). The Pythagoras study: Investigating effects of teaching and learning in Swiss and German mathematics classrooms. In T. Janik & T. Seider (Eds.), The Power of video studies in investigating teaching and learning in the classroom (pp.137-160). Waxmann.
- Klieme, E. & Reusser, K. (2003). Unterrichtsqualität und mathematisches Verständnis im internationalen Vergleich. Ein Forschungsprojekt und erste Schritte zur Realisierung [Teaching quality and mathematical understanding in international comparison. A research project and first steps towards realization]. Unterrichtswissenschaft, 31(3), 194-205
- Klieme, E., Schümer, G., & Knoll, S. (2001). Mathematikunterricht in der Sekundarstufe I: "Aufgabenkultur" und Unterrichtsgestaltung [Mathematics lessons in secondary school: "task culture" and classroom structure]. In E. Klieme & J. Baumert (Eds.), TIMSS - Impulse für Schule und Unterricht (pp. 43-57). Bundesministerium für Bildung und Forschung.
- Kline, R. B. (2016). Methodology in the social sciences. Principles and practice of structural equation modeling (4th ed.). Guilford Press.
- Kunter, M., & Baumert, J. (2007). Who is the expert? Construct and criteria validity of student and teacher ratings of instruction. Learning Environments Research, 9(3), 231–251. https://doi.org/10.1007/s10984-006-9015-7
- Kunter, M., Frenzel, A., Nagy, G., Baumert, J., & Pekrun, R. (2011). Teacher enthusiasm: Dimensionality and context specificity. Contemporary Educational Psychology, 36(4), 289–301. https://doi.org/10.1016/j.cedpsych.2011.07.001
- Kunter, M., Klusmann, U., Baumert, J., Richter, D., Voss, T., & Hachfeld, A. (2013). Professional competence of teachers: Effects on instructional quality and student development. Journal of Educational Psychology, 105(3), 805–820. https://doi.org/10.1037/a0032583
- Kunter, M., Tsai, Y. M., Klusmann, U., Brunner, M., Krauss, S., & Baumert, J. (2008). Students' and mathematics teachers' perceptions of teacher enthusiasm and instruction. Learning and Instruction, 18(5), 468–482. https://doi.org/10.1016/j.learninstruc.2008.06.008
- Lazarides, R., Buchholz, J., & Rubach, C. (2018). Teacher enthusiasm and self-efficacy, student-perceived mastery goal orientation, and student motivation in mathematics classrooms. Teaching and Teacher Education, 69, 1–10. https://doi.org/10.1016/j.tate.2017.08.017
- Lazarides, R., Fauth, B., Gaspard, H., & Göllner, R. (2021). Teacher self-efficacy and enthusiasm: Relations to changes in student-perceived teaching quality at the beginning of secondary education. Learning and Instruction, 73, 101435. https://doi.org/10.1016/j.learninstruc.2020.101435
- Lazarides, R., & Rubach, C. (2017). Instructional characteristics in mathematics classrooms: relationships to achievement goal orientation and student engagement. Mathematics Education Research Journal, 29(2), 201–217. https://doi.org/10.1007/s13394-017-0196-4
- Lazarides, R., & Schiefele, U. (in press). The relative strength of relations between different facets of teacher motivation and core dimensions of teaching quality - A multilevel analysis. Learning and Instruction.
- Lazarides, R., & Watt, H. M. G. (2015). Girls' and boys' perceived mathematics teacher beliefs, classroom learning environments and mathematical career intentions. Contemporary Educational Psychology, 41, 51–61. https://doi.org/10.1016/j.cedpsych.2014.11.005
- LeBreton, J. M., & Senter, J. L. (2008). Answers to 20 questions about interrater reliability and interrater agreement. Organizational Research Methods, 11(4), 815–852. https://doi.org/10.1177/1094428106296642
- Little, R. J. A., & Rubin, D. B. (2002). Statistical analysis with missing data (2nd ed.). Wiley.
- Lüdtke, O., & Trautwein, U. (2007). Aggregating to the between-person level in idiographic research designs: Personal goal research as an example of the need to distinguish between reliability and homogeneity. Journal of Research in Personality, 41(1), 230–238. https://doi.org/10.1016/j.jrp.2006.03.005
- Lüftenegger, M., van de Schoot, R., Schober, B., Finsterwald, M., & Spiel, C. (2014). Promotion of students’ mastery goal orientations: does TARGET work? Educational Psychology, 34(4), 451–469. https://doi.org/10.1080/01443410.2013.814189
- Midgley, C., Maehr, M. L., Hruda, L. Z., Anderman, E., Anderman, L., Freeman, K. E., Gheen, M., Kaplan, A., Kumar, R., Middleton, M. J., Nelson, J., Roeser, R., & Urdan, T. (2000). Manual for the Patterns of Adaptive Learning Scales (PALS). University of Michigan. http://www.umich.edu/~pals/pals/PALS%202000_V13Word97.pdf
- Moè, A. (2016). Does displayed enthusiasm favour recall, intrinsic motivation and time estimation? Cognition & Emotion, 30(7), 1361–1369. https://doi.org/10.1080/02699931.2015.1061480
-
Moè, A., Frenzel, A. C., Au, L., & Taxer, J. L. (2020). Displayed
enthusiasm attracts attention and improves recall. British Journal of Educational Psychology, e12399.
https://doi.org/10.1111/bjep.12399
- Moè, A., & Katz, I. (2020). Emotion regulation and need satisfaction shape a motivating teaching style. Teachers and Teaching, 18, 1–18. https://doi.org/10.1080/13540602.2020.1777960
- Murray, H. G. (1983). Low-inference classroom teaching behaviors and student ratings of college teaching effectiveness. Journal of Educational Psychology, 75(1), 138–149. https://doi.org/10.1037/0022-0663.75.1.138
- Muthén, L., & Muthén, B. (1998-2017a). Mplus (Version 8) [Computer software]. Muthen & Muthen.
- Muthén, L., & Muthén, B. (1998-2017b). Mplus user's guide. Eighth Edition. Muthen & Muthen. https://www.statmodel.com/download/usersguide/MplusUserGuideVer_8.pdf
- Nagy, G., Trautwein, U., Baumert, J., Köller, O., & Garrett, J. (2006). Gender and course selection in upper secondary education: Effects of academic self-concept and intrinsic value. Educational Research and Evaluation, 12(4), 323–345. https://doi.org/10.1080/13803610600765687
- Neugebauer M. (2011) Werden Jungen von Lehrerinnen bei den Übergangsempfehlungen für das Gymnasium benachteiligt? Eine Analyse auf Basis der IGLU-Daten [Are boys being disadvantaged by female teachers when it comes to transition recommendations for the gymnasium? An analysis based on IGLU data]. In: A. Hadjar (Ed.), Geschlechtsspezifische Bildungsungleichheiten (pp. 235-260). VS Verlag für Sozialwissenschaften. https://doi.org/10.1007/978-3-531-92779-4_10
- Opdenakker, M.-C., & van Damme, J. (2006). Teacher characteristics and teaching styles as effectiveness enhancing factors of classroom practice. Teaching and Teacher Education, 22(1), 1–21. https://doi.org/10.1016/j.tate.2005.07.008
- Patrick, B. C., Hisley, J., & Kempler, T. (2000). “What's everybody so excited about?”: The effects of teacher enthusiasm on student intrinsic motivation and vitality. Journal of Experimental Education, 68(3), 217–236. https://doi.org/10.1080/00220970009600093
- Pintrich, P. R. (2000). Multiple goals, multiple pathways: The role of goal orientation in learning and achievement. Journal of Educational Psychology, 92(3), 544–555. https://doi.org/10.1037/0022-0663.92.3.544
- Praetorius, A. K., Klieme, E., Herbert, B., & Pinger, P. (2018). Generic dimensions of teaching quality: The German framework of three basic dimensions. ZDM, 50(3), 407–426. https://doi.org/10.1007/s11858-018-0918-4
- Praetorius, A.‑K., Lauermann, F., Klassen, R. M., Dickhäuser, O., Janke, S., & Dresel, M. (2017). Longitudinal relations between teaching-related motivations and student-reported teaching quality. Teaching and Teacher Education, 65, 241–254. https://doi.org/10.1016/j.tate.2017.03.023
- Rakoczy, K. (2006). Motivationsunterstützung im Mathematikunterricht . Zur Bedeutung von Unterrichtsmerkmalen für die Wahrnehmung von Schülerinnen und Schüler [Support for motivation in mathematics. On the meaning of teaching characteristics for the perception of students]. Beltz.
- Rakoczy, K., Klieme, E., & Pauli, C. (2008). Die Bedeutung der wahrgenommenen Unterstützung motivationsrelevanter Bedürfnisse und des Alltagsbezugs im Mathematikunterricht für die selbstbestimmte Motivation [The impact of perceived support of basic psychological needs and of perceived everyday relevance of contents on students' self-determined motivation in mathematics instruction]. Zeitschrift für Pädagogische Psychologie, 22(1), 25–35. https://doi.org/10.1024/1010-0652.22.1.25
- Raufelder, D., Kittler, F., Braun, S. R., Lätsch, A., Wilkinson, R. P., & Hoferichter, F. (2014). The interplay of perceived stress, self-determination and school engagement in adolescence. School Psychology International, 35(4), 405–420. https://doi.org/10.1177/0143034313498953
- Reeve, J. (2012). A Self-determination theory perspective on student engagement. In S. L. Christenson, A. L. Reschly, & C. Wylie (Eds.), Handbook of research on student engagement (Vol. 34, pp. 149–172). Springer. https://doi.org/10.1007/978-1-4614-2018-7_7
- Reyes, M. R., Brackett, M. A., Rivers, S. E., White, M., & Salovey, P. (2012). Classroom emotional climate, student engagement, and academic achievement. Journal of Educational Psychology, 104(3), 700–712. https://doi.org/10.1037/a0027268
- Rieser, S., Naumann, A., Decristan, J., Fauth, B., Klieme, E., & Büttner, G. (2016). The connection between teaching and learning: Linking teaching quality and metacognitive strategy use in primary school. British Journal of Educational Psychology, 86(4), 526–545. https://doi.org/10.1111/bjep.12121
- Ryan, R.M. & Deci, E.L. (2002). An overview of Self-Determination Theory: An organismic-dialectical perspective. In E. L. Deci & R. M Ryan (Eds.), Handbook of self-determination research (pp. 3-33). University Press.
- Ryan, R. M., &. Deci, E. L. (2020). Intrinsic and extrinsic motivation from a self-determination theory perspective: Definitions, theory, practices, and future directions. Contemporary Educational Psychology, 61. https://doi.org/10.1016/j.cedpsych.2020.101860
- Schiefele, U. (2017). Classroom management and mastery-oriented instruction as mediators of the effects of teacher motivation on student motivation. Teaching and Teacher Education, 64, 115–126. https://doi.org/10.1016/j.tate.2017.02.004
- Schiefele, U., & Schaffner, E. (2015). Teacher interests, mastery goals, and self-efficacy as predictors of instructional practices and student motivation. Contemporary Educational Psychology, 42, 159–171. https://doi.org/10.1016/j.cedpsych.2015.06.005
- Senko, C. (2016). Achievement goal theory: A story of early promises, eventual discords, and future possibilities. In K. Wentzel & D. B. Miele (Eds.), Handbook of motivation at school (2nd ed., pp. 75–95). Routledge.
- Shrout, P. E., & Bolger, N. (2002). Mediation in experimental and nonexperimental studies: New procedures and recommendations. Psychological Methods, 7(4), 422-445. https://doi.org/10.1037//1082-989X.7.4.422
- Skipper, Y., & Douglas, K. (2015). The influence of teacher feedback on children's perceptions of student-teacher relationships. British Journal of Educational Psychology, 85(3), 276–288. https://doi.org/10.1111/bjep.12070
- Tanaka, J. S. (1993). Multifaceted conceptions of fit in structural equation models. In K. A. Bollen & J. S., Long (Eds.), Testing structural equation models (Vol. 154, pp. 10–39). Sage.
- Taxer, J. L., & Frenzel, A. C. (2018). Inauthentic expressions of enthusiasm: Exploring the cost of emotional dissonance in teachers. Learning and Instruction, 53(1), 74–88. https://doi.org/10.1016/j.learninstruc.2017.07.008
- Theis, D., Sauerwein, M., & Fischer, N. (2020). Perceived quality of instruction: The relationship among indicators of students' basic needs, mastery goals, and academic achievement. British Journal of Educational Psychology, 90, 176–192. https://doi.org/10.1111/bjep.12313
- Urdan, T. C., & Schoenfelder, E. (2006). Classroom effects on student motivation: Goal structures, social relationships, and competence beliefs. Journal of School Psychology, 44(5), 331-349. https://doi.org/10.1016/j.jsp.2006.04.003
- Wagner, W., Göllner, R., Helmke, A., Trautwein, U., & Lüdtke, O. (2013). Construct validity of student perceptions of instructional quality is high, but not perfect: Dimensionality and generalizability of domain-independent assessments. Learning and Instruction, 28, 1–11. https://doi.org/10.1016/j.learninstruc.2013.03.003
- Wagner, W., Göllner, R., Werth, S., Voss, T., Schmitz, B., & Trautwein, U. (2016). Student and teacher ratings of instructional quality: Consistency of ratings over time, agreement, and predictive power. Journal of Educational Psychology, 108(5), 705–721. https://doi.org/10.1037/edu0000075
- Waldis, M., Buff, A., Pauli, C., & Reusser, K. (2002). Skalendokumentation zur Schülerinnen- und Schülerbefragung im schweizerischen Videoprojekt [Scale documentation for the student questionnaire in the Swiss video project]. Universität Zürich: Pädagogisches Institut.
- Wang, M.-T., & Fredricks, J. A. (2014). The reciprocal links between school engagement, youth problem behaviors, and school dropout during adolescence. Child Development, 85(2), 722-737. https://doi.org/10.1111/cdev.12138
- Wang, M.-T., Fredricks, J., Ye, F., Hofkens, T., & Linn, J. S. (2019). Conceptualization and assessment of adolescents’ engagement and disengagement in school. European Journal of Psychological Assessment, 35(4), 592–606. https://doi.org/10.1027/1015-5759/a000431
- Wolters, C. A. (2004). Advancing achievement goal theory: Using goal structures and goal orientations to predict students' motivation, cognition, and achievement. Journal of Educational Psychology, 96 (2), 236–250. https://doi.org/10.1037/0022-0663.96.2.236
- Zhang, Q. (2014). Assessing the Effects of Instructor Enthusiasm on Classroom Engagement, Learning Goal Orientation, and Academic Self-Efficacy. Communication Teacher, 28 (1), 44–56. https://doi.org/10.1080/17404622.2013.839047



