Abstract

High throughput biological experiments such as DNA microarrays are very powerful tools to understand and characterize multiple illnesses. These types of experiments, however, have also been described as large, complex, expensive, and hard to analyze. For these reasons, analyses with linear assumptions are frequently bypassed for more sophisticated procedures with higher complexity from the onset. In this work, a search procedure for potential biomarkers using data from microarray experiments is proposed under purely linear assumptions. Linearity offers the possibility of verifiability, convergence and compactness in the selection of a set of potential biomarkers. The method shows a high discrimination rate and does not require the adjustment of parameters by the user, thus preserving analysis objectivity and repeatability. A case study in the identification of potential biomarkers for cervix cancer, as well as a validation study for colon cancer is presented to illustrate the application of the proposed procedure.

Keywords

Cancer biomarkers, microarray experiments

Introduction

An important research objective in biology and the medical sciences is the search for genes whose change in relative expression is an indication of a particular state of an organism such as cancer. These genes are known as biomarkers. Microarray experiments have played an important role in the identification of this type of genes. The successful identification of potential biomarker genes can lead to an eventual clinical confirmation and thus to enhanced disease diagnosis and prognosis capabilities.

Based on our own experience with microarray data, the following challenges regarding microarray experiments can be identified: (1) the available data is highly dimensional in terms of the number of genes to be studied (~10⁴) while showing a scarce number of replicates, (2) there is a rather large variation across replicates, (3) the data is not normally distributed and does not exhibit similar variances, (4) there is a considerable number of missing observations in the majority of experiments, (5) the data is commonly found already being normalized or nonlinearly transformed. All of these complicate the detection of potential biomarkers.

Furthermore, when it comes to data analysis, the following are also important challenges: (i) there is no standard way to compare results for gene selection or identification between studies, (ii) even with the same data (and sometimes with the same technique) different researchers end up with different sets of genes¹, thereby leading to a large number of potential biomarkers to be investigated, the research of which could prove lengthy and very expensive.

Truly integrated work across disciplines is not frequent in most microarray analysis works. Biology and Medicine experts are usually left with the burden of using coded analysis tools with a series of parameters of statistical, computational or mathematical nature that significantly affect the outcome of the software packages². This leads to issues in results reproducibility and comparability between studies.

These challenges motivate the search for microarray analysis techniques from which consistent results can be achieved across several experiments and analysts, particularly for the identification of potential biomarkers.

The purpose of this work is to introduce an approach to identify potential biomarkers from the analysis of microarray experiments based solely on linear models and assumptions. One of the uses proposed for this method is to establish a baseline of comparison for the many sophisticated methods with underlying nonlinear assumptions. The use of linearity throughout the analysis makes the method verifiable, repeatable across different analysts, and computationally tractable. In the following sections, the general analysis strategy is described and two illustrative case studies are presented, the first one in cervix cancer and the second one in colon cancer.

Analysis Strategy

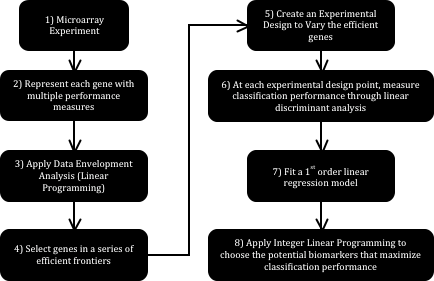
Fig. 1 schematically shows the strategy proposed in this work. Each step is explained below.
Step 1: Microarray Experiment. The process begins with a microarray experiment with m₁ tissues in state one (Control – Cancer-free) and m₂ tissues in state two (Cancer) characterized in n genes. The intersection of each of the n genes with each of the m1+m2 tissues quantifies the relative expression of that particular gene in the selected tissue.

Step 2: Represent each gene with multiple performance measures. Different analysts measure the difference in relative genetic expression across two states differently. P_values are common examples of these measures. A p_value can be computed from the application of a statistical comparison test of a gene’s relative expression in the Control and Cancer states. The Mann-Whitney nonparametric test for the difference of medians of two populations is an instance of such comparisons. Finding an additional p_value for the same gene –since at least two measures are required for each gene- can be done through the removal of a couple of tissues from the microarray experiment under analysis.

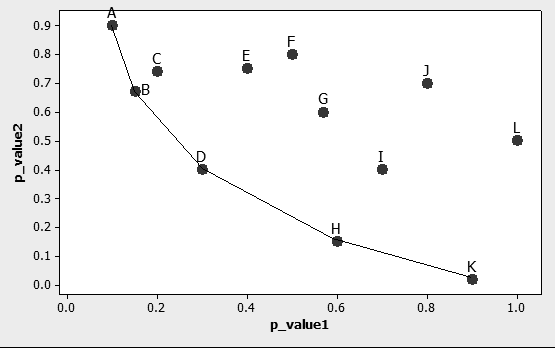
Step 3: Apply Data Envelopment Analysis. Data Envelopment Analysis (DEA) finds the convex envelop of a particular data set consistently and without the need of varying parameters manually. If, for example, two p_values are used to represent each of the n genes in the experiment, then DEA can be used to find the envelope conformed by the dominating genes following the minimization direction of both p_values. Finding such envelope is done through the application of a linear programming formulation, which is the first instance where linearity becomes useful. Fig. 2 schematically shows how this envelope is formed by a series of lines, or in more mathematically correct terms, a series of hyperplanes. Indeed, if only two performance measures are used, it is possible to identify the said envelope graphically with the use of a simple ruler.

Step 4: Select genes in a series of efficient frontiers. The envelopes found through DEA are formally known as efficient frontiers. When an efficient frontier is found, then the solutions lying on it can be removed (as a layer of an onion), to then find the efficient frontier right underneath it. Following this scheme, several layers can be chosen containing different numbers of genes. These genes, having been found through the simultaneous optimization of the chosen performance measures, are the most likely candidates to be biomarkers. These will be referred to as efficient genes.

Step 5: Create an experimental design to vary the presence of the efficient genes. An experimental design that uses the presence of the genes as controllable variables is built in this step. Each variable can take a value of 0 or 1 (0 for absence of the gene). In this case, one run within the experiment corresponds to a combination of efficient genes. Later in the method, this design is used to record the effect of the presence of the said genes in a linear classifier.

Step 6: At each experimental design point, measure classification performance through linear discriminant analysis. Using the experimental design from the previous step, at each combination of efficient genes it is possible to obtain a measure of classification performance using a linear classifier through linear discriminant analysis. A linear classifier of this kind will always converge to the same position, thus preserving results consistency. At the end of this step, then, a complete experimental design relating classification rate with the absence or presence of the potential biomarkers is available.

Step 7: Fit a 1st order linear regression model. With the complete experimental design, it is possible to fit a 1st order linear regression model. This model will relate classification performance (response) to the absence or presence of the efficient genes (independent variables) in an empirical function.

Step 8: Apply integer linear programming to choose the potential biomarkers that maximize classification performance. An optimization problem can be set up in this stage. This problem entails finding the combination of efficient genes –recall that each gene is represented by a variable that can take values of 0 or 1 to indicate absence or presence of that gene- that maximizes the classification performance predicted by the regression model from the previous step.

The linear models and methods explained previously favor repeatability and auditability of results. Furthermore, the set of selected genes do not depend upon the setting of any parameters by the user.

Figure 1. Analysis Strategy based on Linear Models.

Case Study on Cervix Cancer

This case study helps to illustrate the application and the performance of the proposed procedure.

Step 1. The microarray database under analysis is related to cervix cancer and was compiled by Wong et al.³. The database consists of 8 control tissues and 25 cervix cancer tissues, all of them with relative expression level readings for 10,690 genes.

Step 2. The Mann-Whitney nonparametric two-sided test for comparison of medians of two populations was used to generate two different p_values per gene, following a leave-one-tissue-out strategy. This strategy focuses on extracting a particular tissue associated with one state. By removing a tissue, a statistical replicate is effectively deleted from the set, thereby forcing a p_value that is different to the original one. Thus, two different p_values are effectively created to represent each gene. The selection of the tissue to be removed to create a distinct matrix is performed randomly in this instance, however, it can be selected based on the magnitude of its variance (e.g. remove the tissue with the largest variance).

Step 3. The Data Envelopment Analysis model used for this case study was the Banks-Charnes-Cooper (BCC) model⁴. This is a linear programming model with the following associated formulations (P1 and P2):

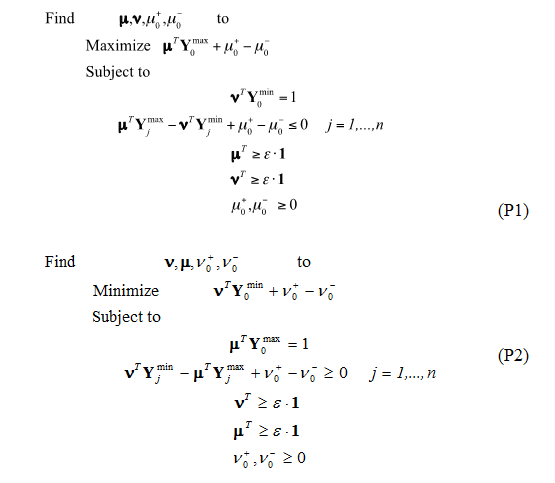
The optimal values of the decision variables correspond to the interceptor and the partial first derivatives (with respect of each performance measure involved) of a supporting hyper plane lying on top of extreme points of the data set under analysis. At the end of the analysis, a piece-wise frontier is distinguishable as shown in Fig. 2. Do notice that, if the analysis requires only two performance measures, this piece-wise frontier can be detected through the superposition of a ruler directly onto the graph.

Figure 2. Representation of genes characterized through two different p_values. Only the case with 2 p_values has a convenient graphical representation, but the analysis can be extended to as many dimensions as performance measures selected.

Step 4. The first ten frontiers were kept for this analysis containing a total of 28 genes. It is important to note the discrimination rate shown by the method already at this point: a reduction of four orders of magnitude in the number of genes to analyze.

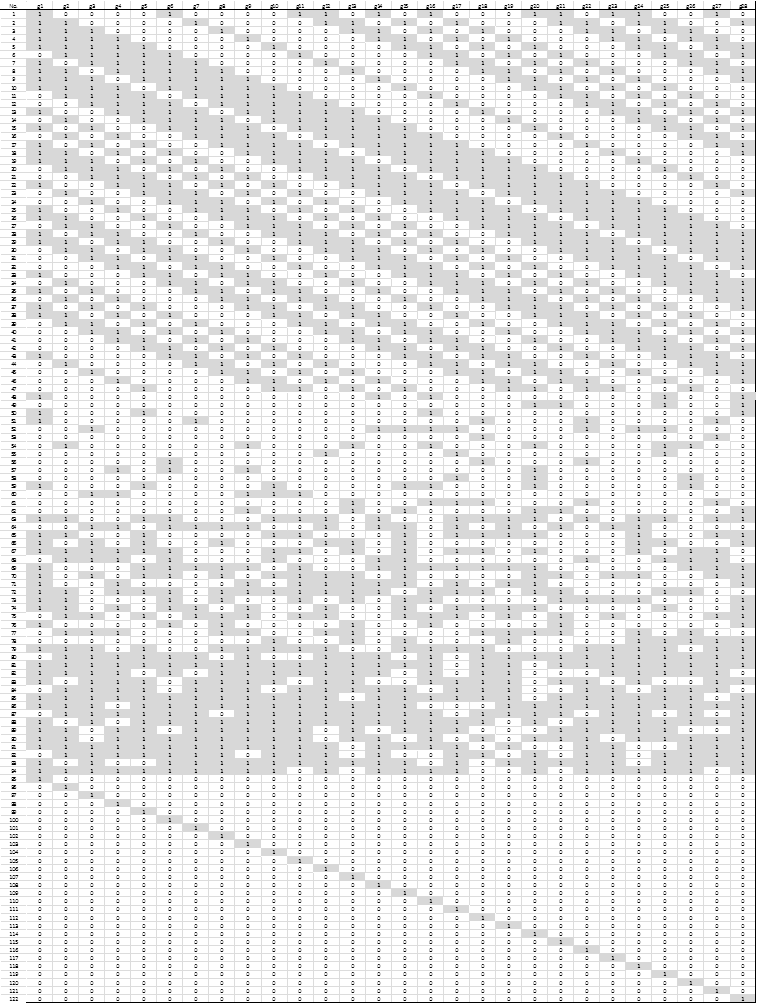
Step 5. In this step a composite experimental design involving 28 binary variables (one per gene in the shortlist from the previous step), was created and used. The experimental design consisted of 122 different runs in which each gene could take a value of 0 (absence) or 1 (presence). In the next step, at each run the analyst will build a linear classifier using only the genes identified with a value of 1 and measure its classification performance. Three different experimental designs form the total of 122 runs. The first design (DOE 1) is an orthogonal array consisting on 47 runs with 10 to 18 genes each; the second design (DOE 2) has 47 runs with 1 to 28 genes generated randomly; and the third design (DOE 3) consisted of 28 runs, each with only one gene. Fig. 3 shows the composite experimental design.

Figure 3. Composite Experimental Design. Values of 1 to indicate the presence of the gene in the associated column are shown shaded.

Step 6. Linear discriminant analysis was carried out using the combination of genes prescribed by each run of the composite design to record the classification performance of a linear classifier. Depending on the absence and presence of certain genes in each run, a range of different classification performances results. It is expected that classification performance improves with more efficient genes present. Using an analogy, a person has a better chance to be identified correctly if more distinctive characteristics of such person are provided. It is also important, however, to search for the minimal number of distinctive characteristics that allows correct classification. This last objective is aided by the next step.

Tables 1-3. Classification performance (CP) for each experimental design

DOE 1			DOE 2			DOE 3
No.	CP		No.	CP		No.	CP
1	0.37		48	0.37		96	0.909
2	1		49	1		97	0.879
3	1		50	1		98	0.879
4	1		51	1		99	0.909
5	1		52	0.909		100	0.879
6	1		53	0.939		101	0.909
7	1		54	0.939		102	0.818
8	1		55	0.939		103	0.879
9	1		56	1		104	0.818
10	1		57	0.939		105	0.879
11	1		58	1		106	0.879
12	1		59	1		107	0.818
13	1		60	1		108	0.848
14	1		61	1		109	0.879
15	1		62	0.97		110	0.879
16	1		63	0.909		111	0.848
17	1		64	1		112	0.939
18	1		65	1		113	0.879
19	1		66	1		114	0.848
20	1		67	1		115	0.788
21	1		68	1		116	0.879
22	1		69	1		117	0.909
23	1		70	1		118	0.758
24	1		71	1		119	0.818
25	1		72	1		120	0.879
26	1		73	1		121	0.818
27	1		74	1		122	0.818
28	1		75	1		123	0.879
30	1		77	1
31	1		78	1
32	1		79	1
33	1		80	1
34	1		81	1
35	1		82	1
36	1		83	1
37	1		84	1
38	1		85	1
39	1		86	1
40	1		87	1
41	1		88	1
42	1		89	1
43	1		90	1
44	1		91	1
45	1		92	1
46	1		93	1
47	1		94	1
			95	1

Step 7. With the experimental design complete, a linear regression of the classification performance as a function of the presence or absence of the 28 genes is built. Noticing that most of the classification performances give a 100% correct classification, two different regression models were constructed (from two different samples). The first one included all of the 122 original runs (DOE 1 + DOE 2 + DOE 3). For the second model, the sample was reduced to only 38 runs, using the 28 runs from DOE 3 and 10 random ones from DOE 2. This was done with the idea of having samples showing a higher sensitivity to the presence of the different genes, as opposed as having mostly runs with a 100% classification performance. With the regression, the relationship between each important gene and the classification performance can be seen as in Equation (1), with variables defined as in Equation (2).

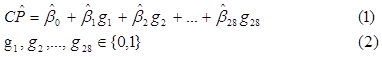
Table 4. Linear regression model using 122 experimental designs

Variable	Coefficient Symbol	Regression Coefficient
	β0	0.8868
g1	β1	0.0152
g2	β2	0.0027
g3	β3	0.0097
g4	β4	0.0146
g5	β5	0.003
g6	β6	0.0083
g7	β7	-0.0034
g8	β8	0.0051
g9	β9	0.0001
g10	β10	0.0054
g11	β11	0.0008
g12	β12	-0.002
g13	β13	0.012
g14	β14	-0.0027
g15	β15	0.0138
g16	β16	0.0089
g17	β17	0.0166
g18	β18	0.0145
g19	β19	0.0089
g20	β20	0.012
g21	β21	0.0137
g22	β22	0.0105
g23	β23	-0.0068
g24	β24	-0.0025
g25	β25	0.0093
g26	β26	0.005
g27	β27	0.0079
g28	β28	0.0158

Table 4 represents the first regression model. A positive regression coefficient indicates that the gene associated to it increases classification performance. Twenty-three different genes have positive coefficients, and thus, contribute to improve classification performance when using all 122 runs to build this first regression model.

Table 5. Linear regression model using 38 experimental designs

Variable	Coefficient Symbol	Regression Coefficient
	β0	0.854962
g1	β1	0.02688
g2	β2	0.01723
g3	β3	0.04222
g4	β4	0.02565
g5	β5	0.02926
g6	β6	0.05826
g7	β7	-0.0345
g8	β8	-0.00439
g9	β9	-0.03323
g10	β10	0.0265
g11	β11	0.0189
g12	β12	-0.01878
g13	β13	0.03906
g14	β14	0.02826
g15	β15	0.04174
g16	β16	-0.02205
g17	β17	0.04799
g18	β18	0.00947
g19	β19	-0.00714
g20	β20	-0.01286
g21	β21	0.01577
g22	β22	0.02561
g23	β23	-0.08053
g24	β24	-0.02284
g25	β25	0.00324
g26	β26	-0.03274
g27	β27	-0.02898
g28	β28	0.0265

After reducing the dataset to only 38 runs the model becomes more targeting. The model represented in Table 5, shows that 17 genes can be used to improve classification performance.

Step 8. Using the two linear regression models described before, the optimization model is to find the combination of genes (through the use of binary variables) to maximize the predicted classification performance using Linear Integer Programming. Formulation P3 shows the resulting optimization problem.

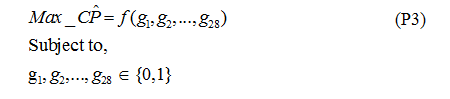
Table 6. Optimization models

Index	Accession Number	Optimization
1	AA488645	x
2	H22826	x
3		x
4	T71316	x
5	AA243749	x
6	AA460827	x
7	AA454831
8	AA913408,     AA913864	x
9	AA487237	x
10	AA446565	x
11	H23187	x
12	AI221445	x
13	R36086	x
14	AA282537
15	N93686	x
16	R91078	x
17	R44822	x
18	AI334914	x
19	R93394	x
20	AA621155	x
21	AA705112	x
22	R52794	x
23	AA424344
24	H69876
25	H55909	x
26	W74657	x
27	AI017398	x
28	H99699	x

Such optimization resulted in the identification of 17 important genes, that is, potential cervix cancer biomarkers. These are shown on Table 6, marked with an ‘x’. Also, a hierarchy of genes can be found using this procedure by sorting them by decreasing magnitude of their regression coefficients. This helps visualize what genes and in which order are most necessary and significant when it comes to detect Cervix Cancer, as shown in Table 7. In this table, CP_Predicted comes from the Classification Performance estimated using the Linear Regression from model 2. CP_Real is the Classification Performance obtained by applying the linear discriminant analysis method.

Table 7. Hierarchy of genes to obtain a maximized classification performance

Hierarchy	Genes	Classification Performance- Predicted	Classification Performance Real
1	6	0.91	0.91
2	17	0.96	0.97
3	3	1.00	0.94
4	15	1.00	0.97
5	13	1.00	0.97
6	5	1.00	1.00
7	14	1.00	1.00
8	1	1.00	1.00
9	10	1.00	1.00
10	28	1.00	1.00
11	4	1.00	1.00
12	22	1.00	1.00
13	11	1.00	1.00
14	2	1.00	1.00
15	21	1.00	1.00
16	18	1.00	1.00
17	25	1.00	1.00

Case Study on Colon Cancer

As part of our study and to reinforce the performance of the proposed method we proceeded to validate the steps illustrated before with another microarray database. The microarray database under analysis for this study was related to colon cancer, made available by Alon, et al.⁵. This database consisted of 22 healthy tissues and 40 colon cancer tissues, all of them with expression level readings of 2000 genes. We kept only 27 genes of the 2000 original genes prevenient of the first ten frontiers founded through DEA. Table 8 shows the resulting efficient genes selected through DEA analysis.

Table 8. Efficient genes prevenient of DEA analysis.

Genes	Frontier	Accession
g1	1	M22382
g2	1	R87126
g3	2	H08393
g4	2	R36977
g5	3	J05032
g6	3	M26383
g7	4	X63629
g8	4	H40095
g9	4	Z50753
g10	4	M63391
g11	5	J02854
g12	5	X12671
g13	6	U09564
g14	6	H43887
g15	6	M76378
g16	7	M36634
g17	7	T86473
g18	8	H06524
g19	8	R84411
g20	8	X14958
g21	9	T92451
g22	9	M26697
g23	9	T71025
g24	10	X86693
g25	10	T47377
g26	10	U30825
g27	10	D31885

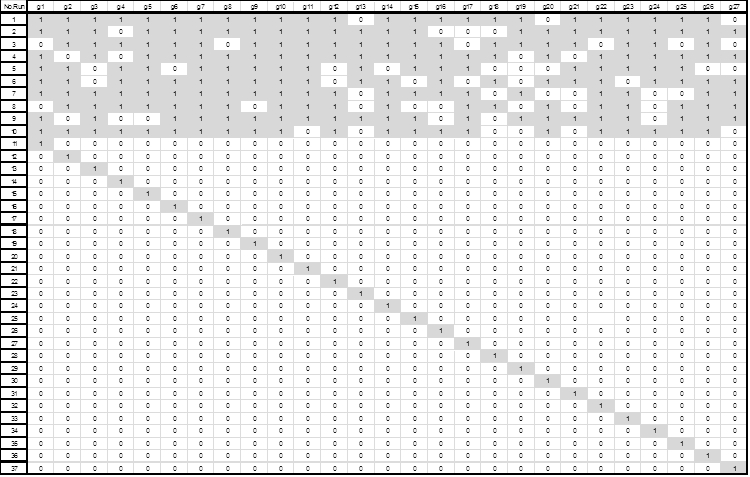
After the identification of these 27 efficient genes, a composite experimental design was created to explore the presence/absence effect of these on a linear classifier. The experimental design involved 27 binary variables and formed 37 runs. The first design consists of 10 runs using between 18 to 24 genes generated randomly; and the second design consisted of 27 runs, each with only one gene activated. Fig. 4 shows the resulting designs.

Figure 4. Composite Experimental Design (10 runs using between 18 to 24 genes generated randomly and 27 runs with only one gene activated). Values of 1 to indicate the presence of the gene in the associated column are shown shaded.

Using the composite experimental design we measured and recorded the classification performance through linear discriminant analysis as shown in Table 9.

Table 9. Classification performances for experimental designs

Run	Classification Performance
1	0.968
2	0.952
3	0.952
4	0.919
5	0.919
6	0.919
7	0.952
8	0.887
9	0.919
10	0.935
11	0.694
12	0.823
13	0.71
14	0.726
15	0.629
16	0.597
17	0.71
18	0.661
19	0.758
20	0.855
21	0.79
22	0.71
23	0.694
24	0.758
25	0.823
26	0.774
27	0.661
28	0.726
29	0.677
30	0.694
31	0.79
32	0.677
33	0.774
34	0.774
35	0.742
36	0.677
37	0.645

After the completion of the experimental designs a linear regression model was used to relate the classification performance with the absence or presence of each of the 27 efficient genes. Fifteen of these genes had a positive regression coefficient, thereby becoming potential colon cancer biomarkers. Table 10 shows a list of these potential colon cancer biomarkers.

Table 10. Genes needed to obtain a 100% classification performance identified through their positive regression coefficients.

Variable	Coefficient Symbol	Regression Coefficient
1	β0	0.716
g1	β1	-0.00379
g2	β2	0.081
g3	β3	0.01
g4	β4	-0.02
g5	β5	-0.1
g6	β6	-0.08
g7	β7	-0.01
g8	β8	-0.03
g9	β9	0.027
g10	β10	0.134
g11	β11	0.068
g12	β12	0.01
g13	β13	-0.05
g14	β14	0.077
g15	β15	0.074
g16	β16	0.036
g17	β17	-0.05
g18	β18	0.01
g19	β19	-0.05
g20	β20	0
g21	β21	0.016
g22	β22	-0.01
g23	β23	0.035
g24	β24	0.01
g25	β25	0.028
g26	β26	0

Once the linear regression analysis was completed, this equation was used to find the combination of genes that maximize the classification performance applying integer linear programming. The use of this tool allowed us to obtain the hierarchy of genes as in the previous example. This hierarchy is shown in Table 11.

Table 11. Hierarchy of genes to obtain a maximized classification performance

Hierarchy	Genes	Prediction	Classification Performance- Real
1	10	0.85	0.855
2	2	0.931	0.855
3	14	1	0.855
4	15	1	0.855
5	11	1	0.855
6	16	1	0.855
7	23	1	0.839
8	25	1	0.871
9	9	1	0.903
10	21	1	0.903
11	3	1	0.919
12	12	1	0.935
13	24	1	0.935
14	18	1	0.935
15	27	1	0.935

Conclusions

In this work, a strategy to detect potential biomarkers from the analysis of microarray experiments is proposed. The strategy is based solely on linear models and assumptions and, as such, is intended as a solid baseline to explore if more complex non-linear based methods bring better results. Its consistent convergence and lack of parameter setting by the users make this method a very competitive and attractive one for repeatability and auditability. This is especially important in high throughput experiments and in a highly interdisciplinary field like bioinformatics. A case study involving the analysis of a microarray database on cervix cancer and validation study on colon cancer were presented to demonstrate the capabilities of the strategy. Indeed, in the studies it was possible to discriminate among more than 10,000 genes to converge to less than 30 potential biomarkers in each case.

Funding

This work was made possible thanks to the NIH-MARC grant “Assisting Bioinformatics Efforts at Minority Institutions” PAR-03-026 and BioSEI UPRM grant 330103080301.

References

1. Ein-Dor L, Kela I, Getz G, et al. Outcome signature genes in breast cancer: is there a unique set? Bioinformatics. 2015;21: 171–178.
2. Pan W. A comparative review of statistical methods for discovering differentially expressed genes in replicated microarray experiments. Bioinformatics. 2002;18: 546–554.
3. Wong YF, Selvanayagam ZE, Wei N, et al. Expression Genomics of Cervical Cancer: Molecular Classification and Prediction of Radiotherapy Response by DNA Microarray. Clin Cancer Res. 2003;9: 5486–5492.
4. Charnes A, Cooper WW, Lewin AY, Seiford LM. Data Envelopment Analysis: Theory, Methodology, and Applications. Boston, MA: Kluwer Academic Publishers;2015.
5. Alon U, Barkai N, Notterman DA, et al. Broad patterns of gene expression revealed by clustering analysis of tumor and normal colon tissues probed by oligonucleotide arrays. Proc Natl Acad Sci USA. 1999;96: 6745–6750.