Abstract

Based upon a two-level structural equation model, this simulation study compares latent variable matching and matching through manifest variables. Selection bias is simulated on latent variable and/or manifest variables along with different magnitudes of reliability. Besides factor score matching and Mahalanobis distance matching, we examined two types of propensity score matching on: “naïve” propensity score derived from manifest covariates, and “true” propensity score derived from latent factor. Results suggest that 1) Mahalanobis distance matching works less effectively than propensity/factor score matching; 2) propensity score and factor score matching performed the best if both treatment and control groups have high reliability; 3) matching through manifest variables is optimal and preferable if latent composite variable is under-representative; 4) when latent variable represents the manifest variables well, latent variable matching is preferable and more efficient than matching on respective manifest variables; and 5) matching options such as caliper matching and replacement matching interact with the magnitude of reliability and matching with replacement on a smaller caliper performs the best for more reliable measures.

Keywords

Measurement error, matching, multi-level, structural equation modeling

Introduction

There is an increasing need for studies on how educational interventions affect student performance (Raudenbush & Sadoff, 2008; Spybrook, 2007). A study’s ability to assess the efficacy and efficiency of educational interventions depends on its hypothesis development, experimental design, controlled experimental trials, identification of the population of interest, and implementation (Sloane, 2008). The most challenging task is to obtain valid measurements of interventions in order to assess the effect of intervention (Raudenbush & Sadoff, 2008; Sloane, 2008). Measures of the classroom interventions that students receive can be subject to measurement errors (Raudenbush & Sadoff, 2008) in data collection through large-scale surveys and observational studies (Cochran,1963, 1965, 1969, 1972; Rosenbaum, 2002).

Structural equation modeling (SEM, Bollen, 1989) incorporates the latent variable to account for measurement errors on manifest variables. Kaplan (1999) applied propensity score stratification into the Multiple Indicators Multiple Causes (MIMIC) model to deal with measurement error on the dependent variable for group difference estimation. However, propensity score matching was not conducted. Furthermore, the propensity score was estimated through observed covariates that may have measurement error. This Monte Carlo study uses an SEM framework (Jöreskog & Sörbom, 1996) to examine the effectiveness of matching through the latent variable and through manifest variables with measurement errors.

Literature Review

Measurement Errors
Measurement errors (Cochran, 1968b) of observed (manifest) variables have been well studied in linear regression (Fuller, 1987), logistic regression (Carroll, Ruppert, Stefanski & Crainiceanu, 2006; Spiegelman, Schneeweiss & McDermott, 1997), and survey sampling (Biemer et al., 2004; Fuller, 1995; Hansen, Hurwitz & Bershad, 1961; Mahalanobis, 1946); however, few studies have been conducted in matching since Cochran and Rubin (1973) reviewed the effect of measurement errors on bias reduction (Rubin, 1973a).

Measurement issues can have serious impact on the findings of a study because they reduce the efficiency of adjustment (Cochran, 1968a; Cochran, 1965). While the literature is replete with guidelines on how to use propensity score analysis (Pan & Bai, 2015) to estimate treatment effect, there is little research on how to adjust the measurement errors to examine bias reduction on covariates after matching (Jakubowski, 2015). Most researchers simply analyze and estimate propensity scores by taking the covariates as the perfect measures (Cochran, 1957; Cochran & Rubin, 1973). Recent propensity score analyses mainly examine how covariates with measurement errors affect treatment effect estimation though bias-correction or imputation (Battistin & Chesher, 2014; Webb-Vargas, Rudolph, Lenis, Murakami & Stuart, 2015), or inverse probability weight (McCaffrey, Lockwook, & Setodji 2011; Steiner, Cook & Shadish 2011). Propensity score matching was rarely conducted in these studies for bias reduction analysis.

Measurement Errors and Bias
Bias occurs when the estimate (testing score or observed treatment effect) differs from the value being estimated (true score or true effect) through sampling (Särndal, Swensson & Wretman, 2003). Bias due to measurement errors (Fuller, 1987) can occur in outcome Y and/or covariates X (Carroll et al., 2006; Cochran & Rubin, 1973). Thus, the outcome in an intervention effect model is a sum of three parts (Wooldridge, 2002): 1) the effect of intervention variety, 2) the effect of initial bias due to covariates X, and 3) the random measurement error. If participants are not randomly assigned to intervention groups (Cochran, 1969, 1972), then a study often has problems of selection bias¹ (Heckman, 1979), indicating the initial unbalanced treatment and control groups in term of covariates X. Selection bias attenuates the treatment effect estimate and misleads one's conclusions (Campbell & Stanley, 1966).

Bias Reduction and Propensity Score Matching
Because the “golden rule" of randomization is generally broken in observational studies (Cochran, 1963, 1965, 1969, 1972; Rosenbaum, 2002), bias reduction techniques have been developed for causal inference (e.g., Rubin, 1974, 1978). These techniques include Cochran's three approaches including pairing, balancing, and stratification (Cochran, 1953), post-hoc matching (Abadie & Imbens, 2006, 2007; Rubin, 1973a,b, 1976a,b, 1979, 1980), analysis of covariance (e.g., Cochran, 1957, 1969), inverse propensity score weighting (Angrist & Pischke, 2009; Horvitz & Thompson, 1952; McCaffrey & Hamilton, 2007), statistical modeling with adjustment (e.g. WLS estimation in HLM frame work, see Hong and Raudenbush, 2006), and double robust estimation using regression adjustment and inverse propensity score weighting (Kang & Schafer, 2007). The most recent development can also be referred to literature and materials in Pan and Bai (2015).

Post-hoc matching depends on the summary measure, a functional composite of covariates (Rubin, 1985). The most commonly used composites in matching include the Mahalanobis distance (e.g., Rubin, 1980) and the propensity score (Rosenbaum and Rubin, 1983). Propensity score matching is a post-hoc bias reduction method, which has been commonly used on observational data to approximate the individual-randomized trials to study a treatment effect of interest (Cochran, 1953, 1968a; Cochran & Rubin, 1973; Rosenbaum & Rubin, 1983; Rubin, 1973a,b). Propensity score matching (Rosenbaum & Rubin, 1983) is the most commonly used bias reduction technique of post-hoc sampling (Cochran, 1953; Rubin, 1973a,b, 1976a,b, 1979, 1980) in causal inference and program evaluation. A propensity score (P) is a conditional probability that an individual belongs to the treatment group (Rosenbaum & Rubin, 1983). It is generally estimated by using the logit model of ln⁡[P/(1 - P)] = β'X, indicating the natural logarithm of the odds (i.e., the ratio of P to 1-P ) is functionally related to the background covariates (X, in a vector format). The propensity score estimated by a function of P^⁡=(1+e-β^^'X)-1, summarizes the distribution information of all potential covariates (Rosenbaum & Rubin, 1983; Rubin, 1985). Using the propensity score, a researcher can match participants from the treatment group with participants from the control group, so that the treatment group and control group can be balanced. This approach can significantly reduce bias in observational study (Rosenbaum, 2005; Rosenbaum & Rubin, 1985; Rubin & Thomas, 1992; Rubin & Waterman, 2006). It also improves the accuracy of the average treatment effect estimate (Abadie & Imbens, 2006), and facilitates causal inference (Greenland, 2004).

Attenuated Bias Reduction Rate Due to Measurement Errors
Measurement errors attenuate the regression coefficient β of covariates X on outcome Y (Fuller, 1987; Jöreskog & Sörbom, 1996). Let β ̃ be the attenuated regression coefficient. It has |β ̃ |<|β| and β ̃=β×R in the bivariate regression (Cochran & Rubin, 1973). R is the attenuation rate due to measurement errors in the covariate x. Bias reduction rate on covariate x is attenuated by R=|β ̃ | ⁄ |β|  due to measurement errors in covariate x (Cochran & Rubin, 1973). The estimation bias reduction rate (Cochran & Rubin, 1973) is computed as 100 (1- treatment effect estimation bias after matching / treatment effect estimation bias before matching)%.

Cochran (Rubin, 2006, p. 20) found that under a simple linear regression, the measurement error on x attenuates the bias reduction rate by a ratio of 1/(1+h). h “ is the ratio of the variance of the errors of measurement to the variance of the correct measurements” (Cochran, 1968b, p. 295). In other words, 1/(1+h) can be rewritten as 1/r, with r representing the reliability.

Measurement-error-adjusted Propensity Scores
When the true covariates (X*) are measured by X with errors, matching needs to be based upon the propensity scores Pr(D = 1|X*) rather than Pr(D = 1|X). There are two ways (Carroll et al., 2006) to adjust for measurement errors in the logit model used to estimate propensity scores.

The first method assumes that the true covariates have not been observed and the naïve parameter estimates are obtained using the observed covariates. An approximately consistent estimator of the parameters is provided through a functional adjustment on the naïve estimator (for details, see Rosner, Spiegelman & Willett, 1990; Rosner, Willett & Spiegelman, 1989). The second method of adjusting for measurement errors in logistic regression is through structural modeling, in which the distribution of the true covariates is parametrically modeled (S¨orbom, 1978; Jakubowski, 2015). For example, the maximum likelihood or Bayesian-approach-based SEM (Carroll et al., 2006; Lee, 2007, Chapter 9) can be used to deal with measurement errors.

This two-step adjusted method requires that X and X* have equal dimensions; however, the measurement-error-adjusted propensity scores cannot be obtained directly using this approach because the integral in the subsequent propensity score function does not have a closed-form solution (Carrel et al., 2006, p. 91). The approximate approach has been developed in Weller, Milton, Eison and Spiegelman (2007) using a multivariate normal conditional distribution of (X*│X, H), H represents the covariates without measurement errors.

Such or similar adjustment has been used in propensity analyses (e.g., Battistin and Chesher 2014; McCaffrey et al., 2011). For example, best linear unbiased predictor (BLUP) corrects measurement error to estimate propensity score using another error-free covariate (McCaffrey et al., 2011, p. 8). However, when the second sample having both X and X* observed is not available, one cannot estimate the measurement-errors-adjusted propensity scores. In this situation, an alternative method such as SEM can be used to estimate the measurement-error-adjusted propensity scores for matching.

Theoretical Framework

Structural equation modeling (Bollen, 1989; Jöreskog & Sörbom, 1996) uses the latent variable to account for measurement errors on manifest variables. Using a two-level SEM (Muthén, 1994), this study manipulates the reliability of the manifest variables to compare latent variable matching with matching through manifest variables.

Structural Equation Modeling as an Alternative
An SEM-based propensity score framework incorporates the latent variable to adjust measurement errors on manifest variables. Propensity scores can be estimated through the following hybrid SEM model:

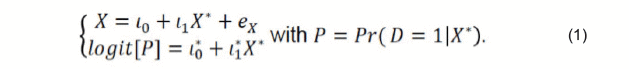
The first equation, a measurement model, captures the linear relationship between the latent X* and observed X in both the treatment (D = 1) and control (D = 0) group. The second equation, a structural model, which is equivalent to the latent variable propensity score model in Equation (2) of Jakubowski (2015, p. 1291). It captures the nonlinear relationship between the latent X* and a latent propensity score. Pr(D = 1|X*)

Adapting a latent variable approach circumvents the post-hoc coefficient adjustment (e.g., Weller et al., 2007) discussed above. The SEM-based propensity scores can be used in matching (Jakubowski, 2015). Note that the latent propensity score Pr(D = 1|X*) and latent X* have a one-to-one functional relationship in the unidimensional case. Matching on estimated propensity scores is mathematically equivalent to matching on the estimated factor scores² of the latent X*.

Factor scores of the latent X* such as academic proficiency measures and ability constructs have been used to match individuals in order to achieve comparable groups (e.g., classical true score in Van der Linden & Hambleton, 1997). The latent construct is measured by multiple manifest items. In the most commonly used item response theory, individual ability is calibrated through a set of test-items with presumptive difficulty and discrimination (Lord & Novick, 1968). The calibrated ability estimation represents an examinee's academic propensity that the set of test-items are designed to measure. However, only matching on latent variables may fail to remove bias due to other omitted covariates H that are free of measurement error. A composite measure such as propensity score that summarizes both the latent X* and covariates H becomes necessary in matching. Wang, Maier and Houang (2017) simulated multi-level data and examined how omitted covariates attenuate the bias reduction rate in the SEM-based propensity score matching. However, the issue of measurement error was not taken into accounted in Wang et al. (see pp. 72-73, 2017). Using the same multi-level SEM-based simulation (Wang, 2015; Wang et al., 2017) and measurement-error-adjusted propensity score model of Equation (1), this study compares latent variable matching and matching through manifest variables to examine the effect of measurement error.

Simulation Study

Longitudinal Design vs. Synthetic Cohort Design
Simulated quasi-experimental synthetic cohort design (SCD, Wiley & Wolfe, 1992) data with measurement errors are generated based on the Second International Mathematic Study (SIMS, International Association for the Evaluation of Educational Achievement, 1977). SIMS used a longitudinal design to study the effects of curriculum and classroom instruction targeted at the 8th grade (Cohort 2). Two waves of mathematic achievement data were collected, at the beginning (Time 0) and end of the school year (Time 1), respectively. Cohort 2 at Time 0 was in the control condition. After the “treatment" of one year of schooling, Cohort 2 at Time 1 data were collected to assess the schooling effect (δ_C2T1-C1T0), defined as the average of “changes in mathematics achievement over the time-span of one school year at the particular grade level" (Wiley & Wolfe, 1992, p. 299).

In practice, Cohort 2 at Time 0 data may not be collected in a study, an alternative cohort Cohort 1 at Time 1 (e.g., grade 7 at Year_i) can serve as the “control” group to estimate schooling effect, denoted now as (δ^_C2T1-C1T1). This design is called the synthetic cohort design (SCD; Wiley & Wolfe, 1992), which has been widely used in aging and epidemiological studies (e.g., Heimberg, Stein, Hiripi, & Kessler, 2000; Kessler, Stein, & Berglund, 1998). Using the synthetic cohort design (SCD), which was used for cross-national comparisons of schooling (Wiley & Wolfe, 1992) in the Third International Mathematics and Science Study 1995 (TIMSS 1995). In this design, the schooling effect is determined by comparing data of two adjacent grades: 7^th (Cohort 1) and 8^th grade (Cohort 2, the focal cohort). The two cohorts are measured at the same time point (Time 1). The SCD by nature is a quasi-longitudinal design, where Cohort 1 at Time 1 data are treated as the “replacement” of Cohort 2 at Time 0 data to estimate schooling effect (δ^_C2T1-C1T1). The schooling effect estimation bias in SCD is

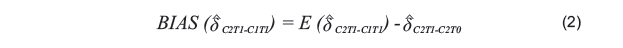
In order to create a quasi-experimental SCD, it is necessary to generate Cohort 1 at Time 1 (7th grade in year i+1) data that are not comparable with Cohort 2 at Time 0 (8th grade in year i) due to measurement errors, so that matching can be used to reduce the simulated selection bias and to decrease the estimation bias of the schooling effect.

The simulation design model is based on data collected in the United States (SIMS-USA, Wolfe,1987), one of the seven countries that collected longitudinal data in SIMS. The final data set includes 126 regular classes and 2,296 students. The average class size is about 27. Tables 1 and 2 list the descriptive statistics of the outcome variables, covariates, and manifest variables. The model selection of variables is based on the previous studies (Schmidt & Burstein, 1992).

Table 1. Level-1 Descriptive Statistics of the Final Two-level Structural Equation Model

Variables	Label	Description	Mean
Educational Inspiration (EDUINSP)	YPWANT	I want to learn more math (inverse code, 1–5a)	4.73
	YPWWELL	Parents want me to do well (1–5a)	4.24
	YPENC	Parents encourage me to do well in math (inverse code, 1–5a)	4.37
Self- encouragement (SLFENCRG)	YIWANT	I want to do well in math (1–5a)	4.32
	YMORMTH	Looking forward to taking more math (1–5a)	3.24
	YNOMORE	Will take no more math if possible (inverse code, 1–5a)	3.73
Family Support (FMLSUPRT)	YPINT	Parents are interested in helping math (inverse code, 1–5a)	3.72
	YFLIKES	Father enjoys doing math (inverse code, 1–5a)	3.53
	YMLIKES	Mother enjoys doing math (inverse code, 1–5a)	3.25
	YFABLE	Father is able to do math homework (inverse code, 1–5a)	3.92
	YMABLE	Mother is able to do math homework (inverse code, 1–5a)	3.71
Math Importance (MTHIMPT)	YMIMPT	Mother thinks math is important (1–5a)	4.60
	YFIMPT	Father thinks math is important (1–5a)	4.55
Socioeconomic Status (SES)	YFEDUC	Father’s education level (1–4a)	3.38
	YMEDUC	Mother’s education level (1–4a)	3.35
	YFOCCN	Father’s occupation national code (1–8a)	4.26
	YMOCCN	Mother’s occupation national code (1–8a)	4.11
Age	XAGE	Grand mean-centered age	0.00
Parental Help	YFAMILY	How frequently family help (1–3a)	1.75
Education Expectation	EDUECPT	YMOREED: Years of education parents expected (1–4a)	2.97
Homework	YMHWKT	Typical hours of math homework per week	2.98

Note: ^a 1 = not at all like, 2 = somehow unlike, 3 = unsure, 4 = somehow like, 5 = exactly like. ^b 1 = little schooling, 2 = primary school, 3 = secondary school, 4 = college or university or tertiary education. ^c 1 =unskilled worker, 2 = semi- unskilled worker, 3 = skilled worker lower, 4 = skilled worker higher, 5 = clerk sales and related lower, 6 = clerk sales and related higher, 7 = professional and managerial lower, 8 = professional and managerial higher. ^d 1 = never/hardly, 2 = occasionally, 3 = regularly. ^e 1 = up to 2 years, 2 = 2 to 5years, 3 = 5 to 8 years, 4 = more than 8 years. N = 2,296.

Table 2. Level-2 Descriptive Statistics of the Final Two-level Structural Equation Model

Variables	Label	Description	Mean
Teacher/Class-level covariates
Class Size	CLASSIZE	Created from the number of students in class	26.60
Opportunity to Learn	OLDARITH	Prior OTL in Arithmetic	7.10
	OLDGEOM	Prior OTL in Geometry	3.19
	NEWALG	This year’s OTL in Algebra	59.61
	NEWGEOM	This year’s OTL in Geometry	41.37
Instruction	TPPWEEK	Number of hours of math instruction per week	5.09
School-level covariates
Qualified Math Teacher Rate	MTHONLY	Proportion of qualified match teachers: Sum of SSPECM and SSPECF divided by STCHS	0.14

Note. N = 126.

Simulated Two-level Structural Equation Model
The proposed two-level SEM (Muthén, 1994) is shown in Figure 1. In the level-1 equation, the post-test score is predicted by the pre-test score, which is predicted by four student characteristics and five latent variables. The latent constructs and their manifest variables are listed in Table 1. In the level-2 model, the intercept of pre-test (β₀) is predicted by four class-/school-level variables. The intercept of the post-test (α₀) is predicted by β₀ and three class-level variables. The level-1 and level-2 residuals are mutually independent of one another.

Figure 1. Two-level structural equation model

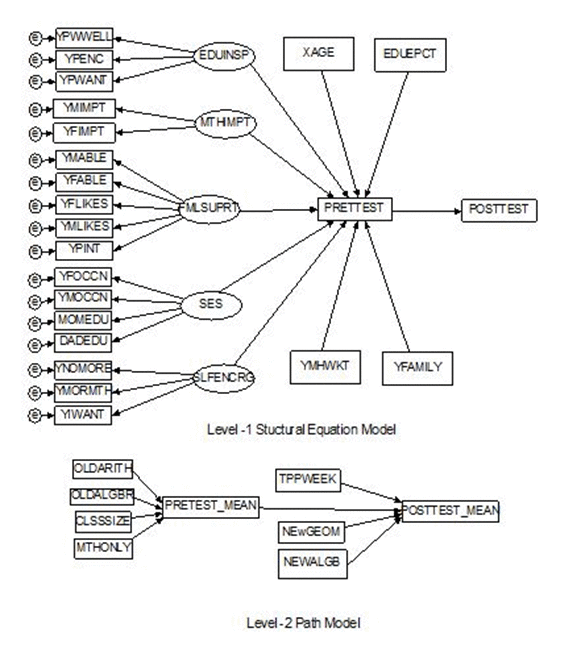
Mplus (Muthén & Muthén, 1998-2015) is used to estimate factor loadings, regression coefficients, and residual variances (see Appendix). These model-based estimates are treated as known parameter values to generate longitudinal data of Cohort 2 at Time 0 and Time 1. The population level SES variables are manipulated using Equation (6) in the simulation descriptions below. Our data-driven approach borrows the “sampling study” metric from MacCallum, Roznowski and Necowitz (1992), who treated the observed data as the “population”, from which random samples were drawn for simulation. Our approach differs from theirs in that we created a hypothetical population from which to draw data for simulation. The SIMS-USA data are collected to represent 3,681,939 8th graders nested in 136,368 classes across the seven strata in the United States (Wolfe, 1987). The simulated pseudo-population includes 12,600 classes and 345,000 students with an average class-size of 27.13.

Table 3. Four Simulations of Matching on Latent and Manifest Variables

Simulation	Cohort 2 Time 0 (8th Grade in Year i)					Cohort 1 Time 1 (7th Grade in Year i+1)
	µXSES	Latent   ηSES	Reliability	ICC		µXSES	Latent   ηSES	Reliability	ICC
				Pre	Post				Pre	Post
One	µ	0	Low	.32	.34	µ + c1	0	Low	.31	.33
Two	µ	0	Low	.32	.34	µ	0	High	.31	.33
Three	µ	0	Low	.32	.34	µ + c2	.68	High	.31	.33
Four	µ	0	High	.32	.34	µ + c2	.68	High	.31	.33

Note: ICC: Intraclass Correlation, which varied from 0.023 to .322 in the most commonly used large-scale surveys on hieratically structured data (Hedges & Hedberg, 2007).

Due to its practical importance in education studies, only latent variable SES and its four manifest variables are manipulated to simulate selection bias. In this study, selection bias is indicated by the non-comparability between Cohort 2 at Time 0 (the treatment group) and Cohort 1 at Time 1 (the control).

Generated Treatment Group Cohort 2 at Time 0 Data
The manifest variables of the latent variable SES are generated through a multivariate normal distribution. The latent variable SES η_SES is associated with 4 manifest variables X_SES^C2T0 through the measurement model

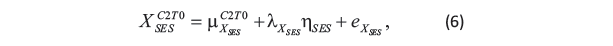
with e_XSES and η_SES ~ N(0,Φ_SES).X_SES^C2T0 includes Father’s/ Mother’s education level (YFEDUC/YMEDUC), and Father’s/ Mother’s occupation national code(YFOCCN/YMOCCN). They are generated through a multivariate normal distribution, X_SES^C2T0 ~ MN(μ_XSES^C2T0,Σ_XSES^C2T0).

The four means are denoted as μ_XSES^C2T0 = [3.375, 3.349, 4.277, 4.128]. The variance matrix Σ_XSES^C2T0 is computed by λ_XSES Φ_SES λ'_XSES + Θ_XSES. The parameter values of λ_XSES, Φ_SES and Θ_XSES are available in the Appendix. The computed variances of Σ_XSES^C2T0) are 0.475, 0.405, 4.421, and 3.916. The reliability coefficient (Lord & Novick, 1968; Raykov, 1997) was computed as 0.25 in Cohort 2 at Time 0.

Generated Control Group Cohort 1 at Time 1 Data
Data generation of Cohort 1 at Time 1 involves manipulating random measurement errors and reliability values to simulate selection bias. The four manipulations are summarized in Table 3. Each manipulation represents one source of simulated selection bias, which causes non-comparability between Cohort 2 at Time 0 data and Cohort 1 at Time 1 data.

Simulation 1: C1T1’s manifest variable means differ from C2T0’s, with the same latent means and low reliability.

In this simulated Cohort 1 at Time 1, the four manifest variables of latent variable SES are generated through a multivariate normal distribution MN(μ_XSES^C1T1, Σ_XSES^C1T1), with μ_XSES^C1T1 = c₁ + μ_XSES^C2T0. Adding c₁ indicates that each manifest variable mean of Cohort 1 at Time 1 is 0.5 standard deviations larger than that of Cohort 2 at Time 0. The four means are denoted as μ_XSES^C2T0 = [3.720, 3.667, 5.328, 5.117]. The computed reliability coefficient for Cohort 1 at Time 1 is equal to 0.25, which is as low as that in Cohort 2 at Time 0. This low reliability has not been examined in the simulated propensity score analysis involved measurement error (reliability of .92 in McCaffrey et al., 2011; reliability from .5 - .9 in Steiner et al., 2011 and Rodriguez de Gil et al., 2015; reliability of .5, .7, .9 and .999 in Webb-Vargas et al., 2015).

Simulation 2: C1T1’s manifest variables have higher reliability than C2T0’s, with the same manifest means and the same latent means.

In the second simulation, the manifest variables of Cohort 1 at Time 1 are generated through a multivariate normal distribution X_SES^C1T1 ~ MN(μ_XSES^C2T0, Σ_XSES^C1T1). The residual variances of the four manifest variables are reduced by 90%. In turn, the computed reliability coefficient is increased to 0.78. A larger reliability coefficient indicates a stronger relationship between the four manifest variables and the latent variable η_SES in Cohort 1 at Time 1. This larger reliability is similar to a value that has been studied in Steiner et al., (2011), Rodriguez de Gil, et al. (2015) and Webb-Vargas et. al (2015).

Simulation 3: C1T1’s manifest variables have higher reliability, with a different latent variable mean from C2T0’s.

In the third simulation, the manifest variables of Cohort 1 at Time 1 have a higher reliability of 0.78; the manifest variables of Cohort 2 at Time 0 have a reliability of 0.25. In addition, the latent variable η_SES means in Cohort 1 at Time 1 is 0.68, which is half of the standard deviation of the latent variable η_SES in Cohort 2 at Time 0. Because of the latent mean difference, the manifest variable means of two cohorts differ by a constant vector c₂. That is, c₂ = 0.68* λ_XSES based on Equation (6) above. In Simulation 1 or 2, the latent variable η_SES mean of Cohort 1 at Time 1 is equal to 0 (see Table 4’s Simulation One and Two).

Simulation 4: C1T1’s latent variable mean differs from C2T0’s, with the same high reliability.

In the fourth simulation, both Cohort 1 at Time 1 and Cohort 2 at Time 0 have a reliability of 0.78. This is achieved by using the manipulation discussed in Simulation 2. The mean of η_SES in Cohort 1 at Time 1 is manipulated in the same way as that discussed in Simulation 3.

Four Types of Matching
The R (R Development Core Team, 2007) module–MatchIt (Ho, Imai, King & Stuart, 2011)– carries out the four types of matching for each manipulation. The first matching, Propensity Score Matching Based on Manifest Variables (PSMMV), uses “naïve” propensity scores estimated through manifest variables. The second, Propensity Score Matching Based on Latent Variable (PSMLV), uses “true” propensity scores estimated from the latent variable. The third, Matching on Factor Score (MFS), treats estimated factor scores as propensity-score-like measures to reduce bias. The factor score is estimated through Mplus (Muthén & Muthén, 1998-2015). The last matching, Mahalanobis Distance Matching Based on Factor Score (MDMFS), uses the Mahalanobis distance of the estimated factor scores. If a unit can be re-used in matching, it is called matching with replacement (Austin, 2014). Using simulated multilevel data, Wang et al. (2017) only conducted matching without replacement and suggested that future study should examine matching with replacement. In our study, each of the four types of matching is conducted with and without replacement. Implementing the same settings in Wang (2015) and Wang et al. (2017), we set up the caliber (Stuart & Rubin, 2008) at 0.2 and 0.01. The simulation design is 4 (simulations) × 4 (types of matching) ×2 (with/out replacement) × 2 (calipers), which determined the structure of Table 4. Each condition is simulated with 1,000 replications. Each replication randomly draws 100 treatment classes and 100 controls, with an average class size of 27. The sample size of each replication on average is 5,400.

Simulation Evaluation
The estimation bias reduction rate (Cochran & Rubin, 1973; Stuart & Rubin, 2008) is computed as:

A larger value bias reduction rate indicates a better performance of matching.

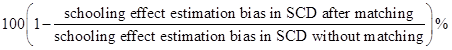
For each of the 1,000 replications, there are four matching methods. In a replication, if the initial bias of the two cohorts is less than 0.5 standard deviations of the 1,000 initial biases, then the two cohorts are comparable and that replication’s matching results will not be used to compute the bias reduction rate. Table 4 summarizes the results of the four manipulation studies.

Table 4: Matching Results of Simulation Design: Four (Simulations)X Four (Types of Matching) X Two (with/out Replacement) X Two (Calipers)

	Four Types of Simulations								Bias Reduction Rate of Four Types of Matching
	C2T0			C1T1
	Observed X¯	Latent Mean	Reliability	Observed X¯	Latent Mean	Reliability	Replacement	Caliper	PSMMV	PSMLV	MFS	MDMFS
One	µ	0	Low (.25)	µ+c1	0	Low (.25)	No	.2	60.77	2.83	2.15	0.60
							No	.01	56.59	-3.38	-2.31	-4.34
							Yes	.2	58.66	-4.59	-4.59	-9.30
							Yes	.01	54.68	-2.64	-2.64	-19.5
Two	µ	0	Low (.25)	µ	0	High (.78)	No	.2	-4.68	0.15	0.59	2.04
							No	.01	2.62	8.35	9.26	5.40
							Yes	.2	5.74	-2.14	3.26	-4.85
							Yes	.01	-4.85	-6.50	-6.50	-16.05
Three	µ	0	Low (.25)	µ+c2	.68	High (.78)	No	.2	50.37	49.46	46.70	4.70
							No	.01	52.65	50.22	49.06	13.98
							Yes	.2	54.47	47.43	47.43	48.87
							Yes	.01	58.53	56.38	56.38	52.68
Four	µ	0	High (.78)	µ+c2	.68	High (.78)	No	.2	55.93	55.10	56.83	3.43
							No	.01	54.93	54.51	54.35	13.74
							Yes	.2	57.11	56.34	56.34	52.22
							Yes	.01	61.95	61.56	61.56	53.03

Note: c₁ represents that each manifest variable mean of Cohort 1 at Time 1 is 0.5 standard deviations larger than that of Cohort 2 at Time 0; c₂ represents that the latent variable mean in Cohort 1 at Time 1 is increased by a half of the standard deviation of the latent variable η_SES in Cohort 2 at Time 0. PSMMV: propensity score matching based on manifest variables; PSMLV: propensity score Matching based on latent variable; MFS: matching on factor score; MDMFS: Mahalanobis distance matching based on factor score.

Results

Simulation 1
In simulation 1, C1T1’s manifest variable means differ from C2T0’s, with the same latent means (0) and low reliability (.25).

Propensity Score Matching Based on Manifest Variables (PSMMV)
Matching on propensity scores estimated from the four manifest variables through a larger caliper (0.2) without replacement reduces the schooling effect estimation bias in SCD (shortened as “estimation bias”) by 60.77%, and with replacement by 58.66%. Matching on a smaller caliper (0.01) without replacement reduces estimation bias by 56.59%, and with replacement by 54.68%.

Propensity Score Matching Based on Latent Variable (PSMLV)
Matching on propensity scores estimated from factor scores through a larger caliper without replacement reduces estimation bias by 2.83%; however, matching with replacement through a larger caliper increases estimation bias by 4.59%. Matching through a smaller caliper without replacement increases estimation bias by 3.38%, and with replacement by 2.64%.

Matching on Factor Score (MFS)
When the estimated factor score is used as a propensity-score-like measure to match through a larger caliper without replacement, it reduces estimation bias by 2.15%, but with replacement increases estimation bias by 4.59%. Matching on a smaller caliper without replacement increases estimation bias by 2.31%, and with replacement by 2.64%.

Mahalanobis Distance Matching Based on Factor Score (MDMFS)
If the estimated Mahalanobis distance of the estimated factor score is used for matching on a larger caliper without replacement, it reduces estimation bias by 0.60%, but with replacement increases estimation bias by 9.30%. Matching on a smaller caliper without replacement increases estimation bias by 4.34%, and with replacement by 19.5%.

In summary, when the latent variable could not represent the manifest variables well (i.e., low reliability), matching based on manifest variable was optimal. Using larger caliper reduced more bias than using smaller caliper. Given the same caliper, matching without replacement reduced more bias than matching with replacement.

Simulation 2
In simulation 2, C1T1’s manifest variables have higher reliability (0.78) than C0T2’s (0.25), with the same manifest means and the same latent means.

Propensity Score Matching Based on Manifest Variables
Matching on propensity scores estimated from the four manifest variables through a larger caliper without replacement increases estimation bias by 4.68%, but with replacement reduces estimation bias by 5.74%. Matching through a smaller caliper without replacement reduces estimation bias by 2.62%, but with replacement increases estimation bias by 4.85%.

Propensity Score Matching Based on Latent Variable
Matching on propensity scores estimated from factor scores through a larger caliper without replacement reduces estimation bias by 0.15%, but with replacement increases estimation bias by 2.14%. Matching through a smaller caliper without replacement reduces estimation bias by 8.35%, but with replacement increases estimation bias by 6.50%.

Matching on Factor Score
Matching on factor scores through a larger caliper without replacement reduces estimation bias by 0.59%, and with replacement by 3.26%. Matching through a smaller caliper without replacement reduces estimation bias by 9.26%, but with replacement increases estimation bias by 6.50%.

Mahalanobis Distance Matching Based on Factor Score
Mahalanobis distance matching based on estimated factor scores through a larger caliper without replacement reduces estimation bias by 2.04%, but with replacement increases estimation bias by 4.85%. Matching through a smaller caliper without replacement reduces estimation bias by 5.40%, but with replacement increases estimation bias by 16.05%.

In summary, when there was no difference between the two groups, matching based on manifest or latent variable was not necessary because little bias was reduced.

Simulation 3
Simulation 3 C1T1’s manifest variables have higher reliability (0.78), and a different latent variable mean (0.68) from C2T0’s (0).

Propensity Score Matching Based on Manifest Variables
Matching on propensity scores estimated from the four manifest variables through a larger caliper without replacement reduces estimation bias by 50.37%, and with replacement by 54.47%. Matching through a smaller caliper without replacement reduces estimation bias by 52.65%, and with replacement by 58.53%.

Propensity Score Matching Based on Latent Variable
Matching on propensity scores estimated from factor scores through a larger caliper without replacement reduces estimation bias by 49.46%, and with replacement 47.43%. Matching through a smaller caliper without replacement reduces estimation bias by 50.22%, and with replacement by 56.38%.

Matching on Factor Score
Matching on factor scores through a larger caliper without replacement reduces estimation bias by 46.70%, and with replacement by 47.43%. Matching through a smaller caliper without replacement reduces estimation bias by 49.06%, and with replacement by 56.38%.

Mahalanobis Distance Matching Based on Factor Score
Mahalanobis distance matching based on estimated factor scores through a larger caliper without replacement reduces estimation bias by 4.70%, and with replacement by 48.87%. Matching through a smaller caliper without replacement reduces estimation bias by 13.98%, and with replacement 52.68%.

Simulation 4
In simulation 4 C1T1’s latent variable mean (0.68) differs from C2T0’s (0), with the same high reliability (0.78).

Propensity Score Matching Based on Manifest Variables
Matching on propensity scores estimated from the four manifest variables through a larger caliper without replacement reduces estimation bias by 55.93%, and with replacement by 57.11%. Matching through a smaller caliper without replacement reduces estimation bias by 54.93%, and with replacement by 61.95%.

Propensity Score Matching Based on Latent Variable
Matching on propensity scores estimated from factor scores through a larger caliper without replacement reduces estimation bias by 55.10%, and with replacement by 56.34%. Matching through a smaller caliper without replacement reduces estimation bias by 54.51%, and with replacement by 61.56%.

Matching on Factor Score
Matching on factor scores through a larger caliper without replacement reduces estimation bias by 56.83%, and with replacement by 56.34%. Matching through a smaller caliper without replacement reduces estimation bias by 54.35%, and with replacement by 61.56%.

Mahalanobis Distance Matching Based on Factor Score
Mahalanobis distance matching based on estimated factor scores through a larger caliper without replacement reduces estimation bias by 3.43%, and with replacement by 52.22%. Matching through a smaller caliper without replacement reduces estimation bias by 13.74%, and with replacement by 53.03%.

In summary, when the latent variable represented the manifest variables well in both treatment and control groups, matching based on manifest and latent variable were equally optimal. Compared with Simulation 3’s results, using a more reliable control group (C2T0) in Simulation 4’s matching achieved the most optimal results. Matching with replacement and smaller caliper was the best choice. Matching with replacement outperformed matching without replacement. In matching without replacement, using larger caliper reduced more bias than using smaller caliper. For matching with replacement, using smaller caliper reduced more bias. Given the same caliper, matching with replacement reduced more bias than matching without replacement. Mahalanobis matching was the least efficient among the four matching methods. And, it was optimal only when matching with replacement was used; and using smaller caliper reduced more bias than larger caliper.

Discussion and Conclusion

Matching on Factor Score Works Sufficiently and Better with Higher Reliability
Measurement error has a negative effect on bias reduction through a latent variable matching framework. If a latent variable, rather than measurement error, mainly accounts for the variation among manifest variables, then matching through the latent variable itself will be equivalent to matching through the propensity score that was computed from the latent variable. This result supports the previous practice of using latent ability or academic proficiency estimates to match treatment and control cohort participants (e.g., Van der Linden & Hambleton, 1997). Latent variable matching will achieve a better bias reduction result if the treatment and control cohorts both have high reliability measures than if either the treatment or control group has a high reliability measure. In cases that involve multi-manifest variables, latent variable matching will be preferable because it is more efficient than matching on respective manifest variables. It is worth noting that latent variable matching approaches are effective if the two cohorts' factor score means are different. If, however, the two cohorts are comparable in terms of the latent variable means, then matching through the latent variable is not necessary.

Matching Based on Manifest Variables with Measurement Error Is Sufficient
In practice, studies often use different quality and types of data in terms of measurement reliability, which requires different matching options and leads to inconsistent results. Measurement error has a case-by-case effect on propensity matching and does not necessarily attenuate the causal effect (Battistin & Chesher, 2014). Naïve propensity score can work as well as other error-corrected propensity score methods (McCaffrey et al., 2011). Webb-Vargas et al. (2015) also found that using naïve covariate and imputation based method worked equally well in propensity score analysis on real data. Findings in Jakubowski (2015) were inconsistent. Matching based on manifest variable can work slightly worse (Table 3 Model B and C, p. 1302) than matching based on latent variable. However, matching based on manifest variable can work slightly better when reliability is the lowest due to measurement error variance and lack of common support (Table 3 Model D, p. 1302). Using manifest variable with measurement error for propensity score analysis can show advantage of bias reduction on treatment effect estimation, specifically when the latent composite variable is under-representative in observational studies. This study is focused on the bias reduction on the covariate rather than the treatment effect estimation. We found that manifest variable based propensity score matching works comparably to latent variable based propensity score matching.

Measurement Complexity and Mixed Matching Effects Request More Latent Variable Based Research on the Topic
This study demonstrates a complicated picture of matching through manifest variables and/or a latent variable because selection bias may be due to the intercept, latent variable and measurement error as shown in Equation (6). Simulation One indicates that matching on manifest variables out-performs matching on the latent variable. That is, if the two cohorts are different only on poorly measured manifest variables with considerable error, then latent variable matching works inefficiently to balance the manifest variables; however propensity score matching through these manifest variables is still optimal. In this situation, selection bias on covariate is NOT due to the latent variable, but measurement error. Then latent variable based propensity score matching is not sufficient to reduce selection bias on covariate. However, manifest variable based propensity score matching will work, because manifest variable contains an extra latent variable, i.e., measurement error. In practice, if the treatment and control groups are hypothesized to have the same distribution of latent ability, matching on propensity score estimated though manifest variables (e.g., observed performance measures) should be practical and optimal.

Matching Options (Replacement and Caliper) Interact with Measurement Reliability
Matching options include whether matching allows replacement and whether a smaller caliper is used. Austin (2011) found that optimal bias reduction rates are obtained when the caliper is in a range from 0 to 0.4 (p. 153). Lunt (2014) recommended to use a tighter caliper because bias reduction performance is worsened when the caliper becomes larger. Austin (2014) simulated non-hierarchical data found that matching with replacement performed as well as caliper matching without replacement. Wang et al. (2017) found that caliper matching interacts with data structure. They recommended that “different sizes of caliper should be used for level-1 [i.e., student-level] and level-2 [i.e., class-level] matching (p. 67) ”. Our student-level matching results showed an interaction between matching options and data quality (i.e., measurement reliability). When measures for the two cohorts have equally low reliability, either using a larger caliper or matching without replacement will reduce more bias; matching without replacement on a larger caliper is optimal. However, the trend is reversed when the two cohorts have equally high reliability. That is, either using a smaller caliper or matching with replacement improves matching performance; and matching with replacement on a smaller caliper performs the best.

Mahalanobis Distance Matching Is Comparatively Nonsufficient
Previous studies have found that post-hoc matching depends on the summary measure that is a functional composite of covariates (Rubin, 1985). The most commonly used composites are the Mahalanobis distance (e.g., Rubin, 1980) and the propensity score (Rosenbaum & Rubin, 1983). Mahalanobis distance matching is less effective than propensity matching on multilevel data (Wang, 2015). Similarly, this study found that Mahalanobis distance matching reduces bias less effectively than either propensity score matching or factor score matching. Mahalobis matching with replacement was comparatively optimal only when the treatment group data are highly reliably. Propensity score matching generally performs better than Mahalanobis distance matching when the true propensity score model is known and the sample size is large (Sekhon & Diamond, 2008). The simulation settings of this study favor propensity score matching. Each simulated condition determines a “true” and known propensity score model. Each of the 1000 replications uses 100 classes, and the sample size is approximately as large as 5,400.

Needs to Examine Both Level-1 and Level-2 Data With Measurement Errors
In educational studies, researchers often sample larger units from a hierarchically structured population (Cochran, 1963; Scott & Smith, 1969). Due to the hierarchical structure of the experimental design and data collection (Raudenbush & Sadoff, 2008), treatment units are generally classes or schools rather than individual students (Hedges, 2007). When clusters are assigned to interventions, non-comparable treatment-control groups can arise from either level-1 or level-2 covariates (Raab & Butcher, 2001), resulting in selection bias. This study focuses on manifest variables and the latent variable only at level-1, although the simulated model is based on a two-level latent variable framework. Future research should explore how level-2 measurement errors will affect the accuracy of matching in terms of the bias reduction rate when level-2 matching and dual matching (Wang, 2015) are needed.

Funding

This study is based on work supported by the National Science Foundation (NSF) under Grant No. DUE-0831581. Any opinions, findings, conclusions or recommendations expressed in this material are those of the author and do not necessarily reflect the views of the NSF.

Appendix

Two-Level Structural Equation Model Estimates (a.k.a True Pseudo-population Parameter Values)

Level One Parameters
Variable	Label	Loading Coefficient			Regression Coefficient						Residual Variance
					PRETEST			POSTTEST
		Coef.	SE	p	Coef.	SE	p	Coef.	SE	p	Est.	SE	p
Pre-Test Score	PRETEST	-	-	-	-	-	-	.72	.03	.00	31.87	1.94	0.00
Post-Test Score	POSTTEST	-	-	-	-	-	-	-	-	-	25.64	1.27	0.00
Educational Inspiration (EDUINSP)	YPWANT	1.00	-	-	.87	1.56	.58	-	-	-	.21	.01	0.00
	YPWWELL	1.05	.08	.00							.37	.03	0.00
	YPENC	1.82	.11	.00							.66	.05	0.00
Self- encouragement (SLFENCRG)	YIWANT	1.00	-	-	1.97	.56	.00	-	-	-	.58	.04	0.00
	YMORMTH	1.98	.18	.00							.67	.05	0.00
	YNOMORE	1.67	.13	.00							.77	.05	0.00
Family Support (FMLSUPRT)	YPINT	1.00	-	-	-.04	.25	.88	-	-	-	.62	.04	0.00
	YFLIKES	.77	.05	.00							.73	.03	0.00
	YMLIKES	.46	.04	.00							1.05	.04	0.00
	YFABLE	1.00	.06	.00							.85	.05	0.00
	YMABLE	.60	.05	.00							1.27	.05	0.00
Math Importance (MTHIMPT)	YMIMPT	1.00	-	-	-.89	.76	.25	-	-	-	.17	.02	0.00
	YFIMPT	1.06	.05	.00							.24	.03	0.00
Socioeconomic Status (SES)	YFEDUC	1.00	-	-	1.55	.30	.00	-	-	-	.17	.01	0.00
	YMEDUC	.72	.04	.00							.24	.01	0.00
	YFOCCN	1.94	.13	.00							3.26	.13	0.00
	YMOCCN	1.54	.14	.00							3.18	.13	0.00
Age	XAGE	-	-	-	-.06	.02	.00	-	-	-	-	-	-
Parental Help	YFAMILY	-	-	-	-1.44	.16	.00	-	-	-	-	-	-
Ed. Expectation	EDUECPT	-	-	-	1.28	.17	.00	-	-	-	-	-	-
Homework	YMHWKT	-	-	-	-.03	.01	.01	-	-	-	-	-	-
Level Two Parameters
Class Size	CLASSIZE	-	-	-	-.20	.06	.00	-	-	-	-	-	-
Opportunity to Learn	OLDARITH	-	-	-	.65	.36	.07	-	-	-	-	-	-
	OLDGEOM	-	-	-	.79	.94	.41	-	-	-	-	-	-
	NEWALG	-	-	-	-	-	-	-.27	.13	.03	-	-	-
	NEWGEOM	-	-	-	-	-	-	.37	.14	.01	-	-	-
Instruction	TPPWEEK	-	-	-	-	-	-	.08	.02	.00	-	-	-
Qualified Math Teacher Rate	MTHONLY	-	-	-	4.51	2.11	.03	-	-	-	-	-	-

Footnotes
¹ Selection bias, also called “sample selection bias” (Heckman, 1979), refers to the bias that is due to the use of non-random samples in estimating relationships among variables of interests. It can occur in two situations: 1) self-selection by objects being studied, and 2) sample selection by researchers or data analysts. Using selection-biased samples results in a biased estimate of the effect of an intervention that should have been randomly assigned. The intervention can refer to “treatment of migration, manpower training, or unionism” (Heckman, 1979, p. 154).
² The estimated factor scores can be derived using SEM software packages such as Mplus (Muthén & Muthén, 1998-2015)

References

• Abadie, A., & Imbens, G.W. (2006). Large sample properties of matching estimators for average treatment effects. Econometrica, 74(1), 235–267. http://dx.doi.org/10.1111/j.1468-0262.2006.00655.x
• Abadie, A., & Imbens, G.W. (2007). Bias-corrected matching estimators for average treatment effects. Retrieved from: http://ksghome.harvard.edu/aabadie/research.html
• Angrist, J.D. and Pischke, J.S. (2009). Mostly harmless econometrics: an empiricist's companion. Princeton, NJ: Princeton University Press.
• Austin, P.C. (2011). Optimal caliper widths for propensity‐score matching when estimating differences in means and differences in proportions in observational studies. Pharmaceutical statistics, 10(2), 150–161. http://dx.doi.org/10.1002/pst.433
• Austin, P.C. (2014). A comparison of 12 algorithms for matching on the propensity score. Statistics in Medicine, 33(6), 1057–1069. http://dx.doi.org/10.1002/sim.6004
• Battistin, E., & Chesher, A. (2014). Treatment effect estimation with covariate measurement error. Journal of Econometrics, 178(2), 707–715. https://doi.org/10.1016/j.jeconom.2013.10.010
• Biemer, P.P., Groves, R.M., & Lyberg, L.E. (2004). Measurement errors in surveys. Hoboken, NJ: Willey.
• Bollen, K.A. (1989). Structural equations with latent variables. New York, NY: Willey.
• Campbell, D.T., & Stanley, J.C. (1966). Experimental and quasi-experimental designs for research. Chicago, USA: Rand McNally College Publishing.
• Carroll, R.J., Ruppert, D., Stefanski, L.A., & Crainiceanu, C.M. (2006). Measurement error in nonlinear models:A modern perspective. Boca Raton, FL: CRC Press.
• Cochran, W.G. (1953). Matching in analytical studies. American Journal of Public Health, 43(6), 684–691.
• Cochran, W.G. (1957). Analysis of covariance: Its nature and uses. Biometrics, 13 (3), 261–281.
• Cochran, W.G. (1963). Sampling techniques. New York, NY: Willey.
• Cochran, W.G. (1965). The planning of observational studies of human populations (with discussion). Journal of the Royal Statistical Society.< Series A (General) 128(2), 234–255.
• Cochran, W.G. (1968a). The effectiveness of adjustment by subclassification in removing bias in observational studies. Biometrics, 24 (2), 295–313.
• Cochran, W.G. (1968b). Errors of measurement in statistics. Technometrics, 10 (4), 637–666.
• Cochran, W.G. (1969). The use of covariance in observational studies. Applied Statistics, 18 (3), 270–275
• Cochran, W.G. (1972). Observational studies. In T. A. Bancroft (Ed.), Statistical papers in honor of george w. snedecor (p. 71-90). Ames, IA: Iowa State University Press.
• Cochran, W.G., & Rubin, D.B. (1973). Controlling bias in observational studies: A review. Sankhy : The Indian Journal of Statistics, Series A, 35, 417–446.
• Fuller, W.A. (1987). Measurement error models. New York, NY: John Wiley & Sons.
• Fuller, W.A. (1995). Estimation in the presence of measurement error. International Statistical Review/Revue Internationale de Statistique, 63(2), 121–141.
• Greenland, S. (2004). An overview of methods for causal inference from observational studies. In A. Gelman & X.-L. Meng (Eds.), Applied bayesian modeling and causal inference from Incomplete-Data perspectives (p. 3–14). New York, NY: Willey.
• Hansen, M.H., Hurwitz, W.N., & Bershad, M.A. (1961). Measurement errors in censuses and surveys. Bull. de Institut. International de Statistique, 38 (2), 359–374.
• Heckman, J.J. (1979). Sample selection bias as a specification error. Econometrica: Journal of the econometric society, 47(1), 153–161.
• Hedges, L.V., & Hedberg, E.C. (2007). Intraclass correlation values for planning group-randomized trials in education. Educational Evaluation and Policy Analysis, 29(1), 60.
• Hedges, L.V. (2007). Correcting a significance test for clustering. Journal of Educational and Behavioral Statistics, 32(2), 151–179.
• Hedges, L. V., & Hedberg, E. C. (2007). Intraclass correlation values for planning group-randomized trials in education. Educational Evaluation and Policy Analysis, 29(1), 60–87.
• Ho, D.E., Imai, K., King, G., & Stuart, E.A. (2011). MatchIt: nonparametric preprocessing for parametric causal inference (version 2.211)[software]. Journal of Statistical Software, 42(8). Available at http://imai.princeton.edu/research/les/matchit.pdf.
• Hong, G. & Raudenbush, S.W. (2006). Evaluating kindergarten retention policy. Journal of the American Statistical Association, 101(475): 901–910.
• Horvitz, D.G. and Thompson, D.J. (1952). A generalization of sampling without replacement from a finite universe. Journal of the American Statistical Association, 47(260), 663–685.
• International Association for the Evaluation of Educational Achievement (1977). The Second International Mathematics Study. Amsterdam: Available at http://www.iea.nl/sims.html.
• Jakubowski, M. (2015). Latent variables and propensity score matching: a simulation study with application to data from the Programme for International Student Assessment in Poland. Empirical Economics, 48(3), 1287–1325.
• Jöreskog, K.G., & Sörbom, D. (1996). LISREL 8: User’s reference guide. Lincolnwood, IL: Scientific Software International.
• Kaplan, D. (1999). An extension of the propensity score adjustment method for the analysis of group differences in MIMIC models. Multivariate Behavioral Research, 34(4), 467–492.
• Kang, J.D.Y. and Schafer, J.L. (2007). Demystifying double robustness: a comparison of alternative strategies for estimating a population mean from incomplete data. Statistical Science, 22(4): 523–539.
• Kessler, R.C., Stein, M.B., & Berglund, P. (1998). Social phobia subtypes in the national comorbidity survey. American Journal of Psychiatry, 155(5), 613–619.
• Lee, S.Y. (2007). Structural equation modeling: A bayesian approach. West Sussex, UK: Willey.
• Lord, F.M., & Novick, M.R. (1968). Statistical theories of mental test scores. Massachusett, US: Addison-Wesley Publishing Company.
• Lunt, M. (2014). Selecting an appropriate caliper can be essential for achieving good balance with propensity score matching. American journal of epidemiology, 179(2), 226-235.
• McCaffrey, D. & Hamilton, L. (2007). Value-Added Assessment in Practice: Lessons from the Pennsylvania Value-Added Assessment System Pilot Project. Santa Monica, CA: Rand Corporation,.
• McCaffrey, D.F., Lockwood, J.R., & Setodji, C.M. (2011). Inverse probability weighting with error-prone covariates. Retrieved from the RAND Corporation web site: http://www.rand.org/content/dam/rand/pubs/working_papers/2011/RAND_WR856-1.pdf
• MacCallum, R.C., Roznowski, M., & Necowitz, L.B. (1992). Model modifications in covariance structure analysis: the problem of capitalization on chance. Psychological Bulletin, 111(3), 490–504.
• Mahalanobis, P.C. (1946). A sample survey of after-effects of the Bengal famine of 1943. Sankhy : The Indian Journal of Statistics, 7(4), 337–400.
• Muthén, B.O. (1994). Multilevel covariance structure analysis. Sociological Methods & Research, 22(3), 376–398.
• Muthén, L.K., & Muthén, B.O. (1998-2015). Mplus user’s guide. Los Angeles. CA: Muthén & Muthén
• R Development Core Team. (2007). R: A language and environment for statistical computing. Vienna: R Foundation for Statistical Computing. Vienna, Austria. Retrieved from http://www.R-project.org.
• Raab, G.M., & Butcher, I. (2001). Balance in cluster randomized trials. Statistics in Medicine, 20(3), 351–365.
• Raudenbush, S.W., & Sadoff, S. (2008). Statistical inference when classroom quality is measured with error. Journal of Research on Educational Effectiveness, 1(2), 138–154.
• Raykov, T. (1997). Estimation of composite reliability for congeneric measures. Applied Psychological Measurement, 21(2), 173–184.
• Rodríguez De Gil, P., Bellara, A.P., Lanehart, R.E., Lee, R.S., Kim, E.S., & Kromrey, J.D. (2015). How do propensity score methods measure up in the presence of measurement error? A Monte Carlo study. Multivariate behavioral research, 50(5), 520–532.
• Rosenbaum, P.R. (2002). Observational study. New York, NY: Springer-Verlag.
• Rosenbaum, P.R. (2005). Observational study. In Encyclopedia of Statistics in Behavioral Science, B.S. Everitt & D.C. Howell (Eds.), Chichester, NY: Wiley, 3, 1451–1462.
• Rosenbaum, P.R., & Rubin, D.B. (1983). The central role of the propensity score in observational studies for causal effects. Biometrika, 70(1), 41–55.
• Rosenbaum, P.R., & Rubin, D.B. (1985). Constructing a control group using multivariate matched sampling methods that incorporate the propensity score. American Statistician, 39(1), 33–38.
• Rosner, B., Spiegelman, D., & Willett, W.C. (1990). Correction of logistic regression relative risk estimates and confidence intervals for measurement error: the case of multiple covariates measured with error. American Journal of Epidemiology, 132(4), 734–745.
• Rosner, B., Willett, W.C., & Spiegelman, D. (1989). Correction of logistic regression relative risk estimates for non-random measurement error. Statistics in Medicine, 8(9), 1051–1069.
• Rubin, D.B. (1973a). Matching to remove bias in observational studies. Biometrics, 29(1), 159–183.
• Rubin, D.B. (1973b). The use of matched sampling and regression adjustment to remove bias in observational studies. Biometrics, 29(1), 185–203.
• Rubin, D.B. (1974). Estimating causal effects of treatments in randomised and nonrandomised studies. Journal of Educational Psychology. 66(5), 688–701.
• Rubin, D.B. (1976a). Multivariate matching methods that are equal percent bias reducing, II: maximums on bias reduction for fixed sample sizes. Biometrics, 32(1), 121–132.
• Rubin, D.B. (1976b). Multivariate matching methods that are equal percent bias reducing, I: Some examples. Biometrics, 32(1), 109–120.
• Rubin, D.B. (1978). Bayesian inference for causal effects: The role of randomization. The Annals of Statistics, 6(1), 34–58.
• Rubin, D.B. (1979). Using multivariate matched sampling and regression adjustment to control bias in observational studies. Journal of the American Statistical Association, 74(366), 318–328.
• Rubin, D.B. (1980). Bias reduction using mahalanobis-metric matching. Biometrics, 36(2), 293–298.
• Rubin, D.B. (1985). The use of propensity scores in applied Bayesian inference. Bayesian statistics, 2, 463–472.
• Rubin, D.B. (2006). Matched sampling for causal effects. New York, NY: Cambridge University Press.
• Rubin, D. B., & Thomas, N. (1992). Affinely invariant matching methods with ellipsoidal distributions. The Annals of Statistics, 20(2), 1079–1093.
• Rubin, D.B., & Waterman, R.P. (2006). Estimating the causal effects of marketing interventions using propensity score methodology. Statistical Science, 21(2), 206–222.
• Särndal, C.E., Swensson, B., & Wretman, J. (2003). Model assisted survey sampling. New York, NY: Springer-Verlag.
• Schmidt, W.H. & Burstein, L. (1992). Concomitants of growth in mathematics achievement during the population a school year. In L. Burstein (Ed.), The IEA Study of Mathematics III: Student growth and classroom processes (pp. 309–327). Oxford, UK: Pergamon Press.
• Scott, A., & Smith, T.M.F. (1969). Estimation in multi-stage surveys. Journal of the American Statistical Association, 64(327), 830–840.
• Sekhon, J.S. & Diamond, A. (2008). Genetic matching for estimating causal effects: A general multivariate matching method for achieving balance in observational studies. Retrieved July 18, 2009, from http://sekhon.berkeley.edu/papers/GenMatch.pdf.
• Sloane, F.C. (2008). Randomized trials in mathematics education: Recalibrating the proposed high watermark. Educational Researcher, 37(9), 624–630.
• Sörbom, D. (1978). An alternative to the methodology for analysis of covariance. Psychometrika, 43(3), 381–396.
• Spiegelman, D., Schneeweiss, S., & McDermott, A. (1997). Measurement error correction for logistic regression models with an “alloyed gold standard”. American Journal of Epidemiology, 145(2), 184–196.
• Spybrook, J.K. (2007). Experimental designs and statistical power of group randomized trials funded by the institute of education sciences. Unpublished doctoral dissertation, University of Michigan, Ann Arbor, Michigan.
• Steiner, P.M., Cook, T.D., & Shadish, W.R. (2011). On the importance of reliable covariate measurement in selection bias adjustments using propensity scores. Journal of Educational and Behavioral Statistics, 36(2), 213–236.
• Stuart, E.A., & Rubin, D.B. (2008). Matching with multiple control groups with adjustment for group differences. Journal of Educational and Behavioral Statistics, 33(3), 279–306.
• Van der Linden, W.J., & Hambleton, R.K. (1997). Handbook of modern item response theory. New York, NY: Springer-Verlag.
• Wang, Q. (2015) Propensity score matching on multilevel data. In W. Pan and H. Bai (Eds.) Propensity Score Analysis: Fundamentals and Developments (pp.217–235). New York, NY: Guilford
• Wang, Q., Maier, K. & Houang, R. (2017). Omitted variables, R₂, and bias reduction in matching hierarchical data: A Monte Carlo study. Journal of Statistics: Advances in Theory and Applications, 17(1), 43-81
• Webb-Vargas, Y., Rudolph, K.E., Lenis, D., Murakami, P., & Stuart, E.A. (2015). An imputation-based solution to using mismeasured covariates in propensity score analysis. Statistical Methods in Medical Research, 0(0), 1–17. http://dx.doi.org/10.1177/0962280215588771
• Weller, E.A., Milton, D.K., Eisen, E.A., & Spiegelman, D. (2007). Regression calibration for logistic regression with multiple surrogates for one exposure. Journal of Statistical Planning and Inference, 137(2), 449–461.
• Wiley, D.E., & Wolfe, R.G. (1992). Major survey design issues for the IEA third international mathematics and science study. Prospects, 22(3), 297–304.
• Wolfe, R.G. (1987, March). Second international mathematics study: Training manual for use of the databank of the longitudinal, classroom process surveys for population a in the IEA second international mathematics study. (Contractor’s Report). Washington, D.C: Center for Education Statistics.
• Wooldridge, J.M. (2002). Econometric analysis of cross section and panel data. Cambridge, MA, USA: MIT Press.